Advent of Code 2021攻略ガイド

Advent of Code 2021は，海に落ちた鍵を探しに行く話です．

概要

まずはソナーを使用して鍵を検出できないか試します．ソナーの計測値が時系列データとして次のように与えられます．

199
200
208
210
200
...

Part 1

1つ前の値と比べて増加している計測値の数を回答します．愚直にループで実装すれば問題ありません．

初めての言語で挑戦する場合は，ファイルや標準入力の読み込み方法，数値のパース方法などが求められます．

解答コード

Part 2

計測値のノイズを排除するために，大きさ3のスライディングウインドウを設定し，ウインドウ内の合計値が増加する回数を回答します．こちらも愚直に実装すれば問題ありません．

または，3つ前の値と比べて増加している計測値をカウントしても同じです．

解答コード

概要

潜水艦の動きが次のように与えられます．

forward 5
down 5
forward 8
up 3
down 8
forward 2
...

Part 1

入力値の意味が次のように与えられます．

• forward N: 水平位置がN増加する
• down N: 深さがN増加する
• up N: 深さがN減少する

入力どおりに潜水艦を動かした場合の最終的な位置における， $水平位置 \times 深さ$ を回答します．

特に工夫は必要ありません．入力をパースしながら潜水艦の現在位置を更新して行けば良いです．

解答コード

Part 2

実はPart 1で与えられた入力値の意味が間違っていたと教えられます．本当の意味は次のとおりです．

• down X: AimをX増やす
• up X: AimをX減らす
• forward X: 次のことを行う
  • 水平位置をX増やす
  • $Aim \times X$ だけ深さを増やす

こちらも特に工夫はいりません．

解答コード

概要

潜水艦の調子がおかしいです．診断データが2進数で次のように与えられます．

00100
11110
10110
...

Part 1

消費電力を10進数で求められます．消費電力は $ガンマレート * イプシロンレート$ です．

ガンマレートは入力値の各ビットの最瀕値をくっつけたものになります．イプシロンレートはその逆で，各ビットの最瀕値でないビットをつなげた値になります．

各行をパースしながら，各桁の0と1の度数を集計していき，最後にガンマレートとイプシロンレートを計算すればいいでしょう．

値のパースや基数変換の方法が求められます．

解答コード

Part 2

生命維持率を回答します．生命維持率は，酸素発生率と二酸化炭素吸収率の積です．

生命維持の求め方は少し複雑です．すべての入力値のうち，各ビットの最瀕値を持つもの以外を取り除くという操作をします．

例：

1. 全ての入力値の1ビット目の最瀕値は1
2. 1ビット目が1でない値を取り除く
3. 残りの入力値の2ビット目の最瀕地は0
4. 2ビット目が0でない値を取り除く…

基本的にはそのまま実装すれば問題ありません．

「取り除く」という操作をどのように実現するかは言語によって異なると思います．可変長配列や集合が使えるなら簡単です．使えないなら，各値に「取り除かれたか」というビットを保持しておくなどの方法があるでしょう．

解答コード

概要

ビンゴで遊びたそうなダイオウイカが近づいてきたので，潜水艦になぜか搭載されているビンゴシステムを使って対決します．（未来予知によって確実に勝ちますが）

数字を開ける順番と，複数のビンゴボードが次のように与えられます．

7,4,9,5,11,17,23,2,0,14,21,24,10,16,13,6,15,25,12,22,18,20,8,19,3,26,1 // 数字を開ける順番

22 13 17 11  0
 8  2 23  4 24
21  9 14 16  7
 6 10  3 18  5
 1 12 20 15 19

 3 15  0  2 22
 9 18 13 17  5
19  8  7 25 23
20 11 10 24  4
14 21 16 12  6

14 21 17 24  4
10 16 15  9 19
18  8 23 26 20
22 11 13  6  5
 2  0 12  3  7

Part 1

順番通りに数字を開けていき，一番最初にビンゴするボードにおける得点を回答します．

ビンゴしたボードの得点は， $ビンゴした列の値の合計 \times 数字が呼ばれた回数$ で計算できます．

計算量に関する懸念はないのでそのまま実装していけばOKです．ボードのパースやビンゴ判定の実装が少し大変かもしれません．

解答コード

Part 2

Part 1とは異なり，一番最後にビンゴするボードの得点を回答します．（ボードの得点計算において，「数字の呼ばれた回数」のウエイトが高いので一番最後のボードを選べば勝てる）

Part 1が解けているならほぼ同じコードの流用で解けます．

解答コード

余談

この問題，呼ばれる数字列を自分側があらかじめ知っているのズルくないですか？イカサマでは？（激ウマギャグ）

あと，yosuke_furukawaさんが「イカゲームと掛けたのかなこれは」と言っていましたが， 私は違うと思います．

概要

熱水噴出口の情報から，海水温が高い危険な場所を計算します．

噴出口の情報は次のように与えられます．

0,9 -> 5,9
8,0 -> 0,8
9,4 -> 3,4
2,2 -> 2,1
7,0 -> 7,4
6,4 -> 2,0
0,9 -> 2,9
3,4 -> 1,4
0,0 -> 8,8
5,5 -> 8,2
...

各座標が整数の2次元平面を考えます．ここで，例えば0,9 -> 5,9は，(0,9)から(5,9)へ熱水が吹き出しており，海水温が高いことを表しています．

Part 1

噴出口が重なる位置の数を回答します．つまり，入力の線分の交点の数を回答します．また，このパートでは水平または垂直の噴出口のみを考慮すれば良いです．

2次元配列を用意して，入力の通りに海水温の高い位置をカウントアップしていけば良いです．おそらく計算量的にも問題ない時間で解けます．

一方で，累積和，いもす法を使用することでより早く計算できるかもしれません．今回の問題では線分を扱っているので，あまりメリットが無い気もしますが，私はせっかくなのでいもしてみました．

解答コード

Part 2

Part 1に加えて，斜め方向も考慮せよと言われます．Part 1のコードを少し拡張するだけで解けるはずです．

解答コード

概要

ハダカイワシの成長，増加を計算します．

ハダカイワシは次の規則で成長し，増加します．

• 大人の個体は7日に1ひきの子供を産みます
• 子供は2日で大人になります

つまり，各ハダカイワシには子供を生むまでの「内部タイマー」という概念があり，次のように増えます．

Initial state: 3,4,3,1,2
After  1 day:  2,3,2,0,1
After  2 days: 1,2,1,6,0,8
After  3 days: 0,1,0,5,6,7,8
After  4 days: 6,0,6,4,5,6,7,8,8
After  5 days: 5,6,5,3,4,5,6,7,7,8
After  6 days: 4,5,4,2,3,4,5,6,6,7
After  7 days: 3,4,3,1,2,3,4,5,5,6
...

ここで，パズルの入力として初期値が3,4,3,1,2のように与えられます．

Part 1

80日後のハダカイワシの数を回答します．

遅い方法

一番ナイーブな解法は，各ハダカイワシの内部タイマーを[3,4,3,1,2]のような可変長配列で管理し，一日ごとにすべてのタイマーをデクリメントしながら，0を見つけて子供を追加していく方法です．しかしこの方法は計算コストが高いです．

早い方法

上記の増加表を見ていると，ある時点で同じ内部タイマーを持つイワシは，その後の変化が同じであることに気づきます．つまり，イワシごとの内部タイマーを管理するのではなく，内部タイマーごとのイワシの数を覚えれば十分であることになります．

After  7 days: 3,4,3,1,2,3,4,5,5,6

の場合，

[3,4,3,1,2,3,4,5,5,6]

ではなく

[0,1,1,3,2,2,1,0,0]

を扱う

そして，内部タイマーを減らすためには，配列を左にシフトします．

[0,1,1,3,2,2,1,0,0]

日が経過したので左にシフト

[1,1,3,2,2,1,0,0,0]

添字0の位置が1
→内部タイマー0のイワシが1ひきいる
→1ひきの子供が生まれる
→配列の添字8（右端）に1を加算

...

もうちょっと早い？方法

言語やデータ構造によっては，配列を左シフトするのは高価かもしれません．

親イワシは内部タイマーによって順番に子供を産んでいくので，大人イワシだけの配列を作り，「現在子供を産む大人イワシのポインタ」をループさせれば良いと思いました．「子供イワシ」は別のキューで管理し，大人になったら大人イワシ配列へ追加します．

大人イワシ配列，子供イワシキュー
[0,1,1,3,2,2,1] [0,0]
 ^現在子供を産むイワシ

→子供を産むイワシなし，成長して大人になったイワシなし

[次の日]

[0,1,1,3,2,2,1] [0,1]
   ^現在子供を産むイワシ

→子供を産むイワシ1ひき，成長して大人になったイワシなし

[次の日]

[0,1,1,3,2,2,1] [1,1]
     ^現在子供を産むイワシ

→子供を産むイワシ1ひき，成長して大人になったイワシなし

[次の日]

[0,1,2,3,2,2,1] [1,3]
       ^現在子供を産むイワシ

→子供を産むイワシ1ひき，成長して大人になったイワシ1ひき（現在子供を産むイワシポインタの直前に加算）

...

以下のコードはこの方法で実装されています．

解答コード

Part 2

255日後のイワシの数を回答します．上記のナイーブな実装ではきついはずです．

解答コード

概要

横方向にしか動けないカニの潜水艦を縦に整列させる問題です．（そして，カニ潜水艦から出るビームか何かで海底を破壊するらしいです）

カニ潜水艦の初期位置が16,1,2,0,4,2,7,1,2,14のように与えられます．図示すると以下のようになります．

位置:     0123456789...
潜水艦1:                  #
潜水艦2:   #
潜水艦3:    #
潜水艦4:  #
潜水艦5:      #
潜水艦6:    #
潜水艦7:         #
潜水艦8:   #
潜水艦9:    #
潜水艦10:               #

Part 1

カニ潜水艦は横へ1つ動くのに燃料を1消費します．全体の燃料が最も少なくなる整列位置を回答します．（上記の例では位置2が最もエコらしいです）

全域探索で解きました．すべての位置について消費燃料を計算し，最小値を求めればいいです．もっと効率の良い方法があるかもしれません．

解答コード

Part 2

実はカニ潜水艦は，横へ1つ動くのに燃料1，もう1つ動くのに燃料2，さらに動くのに燃料3を消費するのだそうです．そのうえで全体の燃料が最も少なくなる位置を回答します．

こちらも全域探索でゴリ押して解けました．各潜水艦の消費コストは，等差数列の和の公式を知っていれば $\mathcal{O}(1)$ で求まります．

解答コード

概要

配線がおかしい7セグの表示を復元する問題です．

次のような入力が与えられます．

eadbcf faceb faecgd gdefabc adc ad adbf gfacbe bceda dcegb | gdfcae adc cedbfa dafb
edbfga begcd cbg gc gcadebf fbgde acbgfd abcde gfcbed gfec | fcgedb cgb dgebacf gc
fgaebd cg bdaec gdafb agbcfd gdcbef bgcad gfac gcb cdgabef | cg cg fdcagb cbg
...

潜水艦にはたくさんの7セグ4桁 ディスプレイが搭載されていますが，それぞれで配線がおかしいです．各行は，各4桁7セグディスプレイに関する情報です．

今は1つの行，1つの7セグ4桁 ディスプレイに着目します．

ディスプレイは次のようになっています．

潜水艦からの入力: a b c d e f g
                  | | | | | | |
            [ここで配線が入れ替わっている]
                  | | | | | | |
ディスプレイ入力: a b c d e f g
 aa  |  aa  |  aa  |  aa
b  c | b  c | b  c | b  c
b  c | b  c | b  c | b  c
 dd  |  dd  |  dd  |  dd
e  f | e  f | e  f | e  f
e  f | e  f | e  f | e  f
 gg  |  gg  |  gg  |  gg

つまり，1つのディスプレイ内の全ての桁は同じ配線ミスの影響を受けます．このディスプレイに対応する次の入力に着目します．

eadbcf faceb faecgd gdefabc adc ad adbf gfacbe bceda dcegb | gdfcae adc cedbfa dafb

行の右側は，現在点灯しているディスプレイ側のセグを表しています．1桁目はcdfeb，2桁目はfcadb…が点灯しています．

潜水艦からの入力: a b c d e f g
                  | | | | | | |
            [ここで配線が入れ替わっている]
                  | | | | | | |
ディスプレイ入力: a b c d e f g
 ##  |  ##  |  ##  |  ##
.  # | .  # | #  # | #  .
.  # | .  # | #  # | #  .
 ##  |  ##  |  ##  |  ##
#  # | .  . | #  # | .  #
#  # | .  . | #  # | .  #
 ##  |  ..  |  ..  |  ..

配線がおかしいので表示がめちゃくちゃです．

入力行の左側は，表示されうるディスプレイ側のパターンを表しています．0〜9の10パターンあります．つまり，adはディスプレイのaとdが同時に表示されうることを表します．

このようなディスプレイが入力行の数だけ潜水艦に設置されています．

Part 1

潜水艦の全てのディスプレイに1, 4, 7, 8がいくつ表示されているか求められます．これらの数字は，表示のために必要なセグ数が固有なので，配線ミスの影響を受けずに識別可能です．

例えば，1を表示するためには2つのセグが必要ですが，0〜9の他の数字で2つのセグのみで表示できるものはありません．

したがって，入力行の右側で2つのセグを使用しているものを数えれば，潜水艦全体の1の個数がわかります．

他の数字に関しても同様に数えるだけです．

解答コード

Part 2

各ディスプレイの表示を解析し，数値の合計値を回答します．

ここでは，ディスプレイ側の各セグごとに「接続されうる潜水艦側のセグ」を管理して解きました．以下の行を例に詳しく説明します．

eadbcf faceb faecgd gdefabc adc ad adbf gfacbe bceda dcegb | gdfcae adc cedbfa dafb

行の左側について，まず表示セグの数ごとに整理します．

//表示セグ2個（表している数字は1）
ad

// 表示セグ3個（表している数字は7）
adc

// 表示セグ4個（表している数字は4）
adbf

// 表示セグ5個（表している数字は2 or 3 or 5）
faceb
bceda
dcegb

// 表示セグ6個（表している数字は0 or 6 or 9）
eadbcf
faecgd
gfacbe

// 表示セグ7個（表している数字は8）
gdefabc

次に，ディスプレイの各セグについて「接続されうる潜水艦側のセグ」を準備します．最初は全ての可能性があるので次のようになります．

ディスプレイセグa: (a, b, c, d, e, f, g)
ディスプレイセグb: (a, b, c, d, e, f, g)
ディスプレイセグc: (a, b, c, d, e, f, g)
ディスプレイセグd: (a, b, c, d, e, f, g)
ディスプレイセグe: (a, b, c, d, e, f, g)
ディスプレイセグf: (a, b, c, d, e, f, g)
ディスプレイセグg: (a, b, c, d, e, f, g)

ここで，例えばadの情報を使うと次のように推論できます．

"ad"は表示に2個のセグを使う
→2個のセグで表示する数字は1しかない
→したがって，ディスプレイセグのaとdには，潜水艦側のcまたはfしか接続され得ない

ディスプレイセグa: (c, f)
ディスプレイセグb: (a, b, c, d, e, f, g)
ディスプレイセグc: (a, b, c, d, e, f, g)
ディスプレイセグd: (c, f)
ディスプレイセグe: (a, b, c, d, e, f, g)
ディスプレイセグf: (a, b, c, d, e, f, g)
ディスプレイセグg: (a, b, c, d, e, f, g)

また，ディスプレイセグのaとd以外に，潜水艦側のcとfが接続されることはない

ディスプレイセグa: (c, f)
ディスプレイセグb: (a, b, d, e, g)
ディスプレイセグc: (a, b, d, e, g)
ディスプレイセグd: (c, f)
ディスプレイセグe: (a, b, d, e, g)
ディスプレイセグf: (a, b, d, e, g)
ディスプレイセグg: (a, b, d, e, g)

続けて，例えばfaceb，bceda，dcegbの情報を使うと次にように推論できます．

"faceb"，"bceda"，"dcegb"に関して，それぞれの表示に5個のセグを使う
→2または3または5の入力である
→それぞれにセグb，c，eが共通して現れている．
→これらは2，3，5の表示に共通して使う部分（以下参照）が接続されているディスプレイセグである
 ##  // #: 共通部分
.  . // .: 非共通部分
.  .
 ##
.  .
.  .
 ##
→つまり，これらのセグには，2，3，5の表示に共通して使わない部分の潜水艦側セグは接続されていない
→ディスプレイセグb，c，eからb，c，e，fを削除

ディスプレイセグa: (c, f)
ディスプレイセグb: (a, d, g)
ディスプレイセグc: (a, d, g)
ディスプレイセグd: (c, f)
ディスプレイセグe: (a, d, g)
ディスプレイセグf: (a, b, d, e, g)
ディスプレイセグg: (a, b, d, e, g)

また，"faceb"，"bceda"，"dcegb"に「現れているが共通していないセグ」には，2，3，5の表示に共通して使う部分の潜水艦側セグは接続されていない
→つまり，"faceb" | "bceda" | "dcegb" - "faceb" & "bceda" & "dcegb"＝"adfg"には，潜水艦側のa，d，gは接続されない
→ディスプレイセグa，d，f，gからa，d，gを削除

ディスプレイセグa: (c, f)
ディスプレイセグb: (a, d, g)
ディスプレイセグc: (a, d, g)
ディスプレイセグd: (c, f)
ディスプレイセグe: (a, d, g)
ディスプレイセグf: (b, e)
ディスプレイセグg: (b, e)

…というようにして，全ての制約を使うと潜水艦側セグとディスプレイセグの対応関係がわかります．あとは，その対応関係と入力行右側の情報を使ってディスプレイに本来表示されるはずだった数値を復元し，それをすべての行に対して実行し，合計を求めました．

効率性や計算量などは問題になりませんでしたが，とにかく上記のアルゴリズムを実装に落とし込むのが大変でした．

解答コード

概要

海底の標高マップから盆地を見つける問題です．海底火山の煙を回避するために，煙の流れを見たいそうです．

次のようなマップが入力されます．

2199943210
3987894921
9856789892
8767896789
9899965678

各数字はその地点の標高です．

Part 1

周囲よりも低い場所のリスクレベルを回答します．リスクレベルは，その位置の$標高 + 1$です．つまり，上下左右の自分自身よりも高い場所について，その標高の合計を数えます．マップの端は反対側と隣接していません．

基本的に全域探索しました．マップの端付近では周囲のセルが3個だったり2個だったりになるので，そのへんだけ注意していれば問題なく解けます．

解答コード

Part 2

盆地を探索します．盆地とは9以外のセルのクラスタです．例えば次のようなものです．

##99943210
#987894921
9856789892
8767896789
9899965678

すべての盆地を面積が大きい順に並べて，最大3つの面積の積を回答します．

まず，盆地の面積を深さ優先探索する次のような関数を作りました．

fn find_basin_cells<'a>(
    point: Point<usize>,
    visited_points: &'a mut HashSet<Point<usize>>,
    map: &'a Map,
) -> &'a mut HashSet<Point<usize>>

そして，マップのすべての位置に対してこの関数を実行して盆地を探索しました．

解答コード

概要

カッコを数える問題です．入力は次のようなものです．

[({(<(())[]>[[{[]{<()<>>
[(()[<>])]({[<{<<[]>>(
{([(<{}[<>[]}>{[]{[(<()>
...

各開きカッコはそれぞれの閉じカッコに対応します．

入力の各行には，カッコの対応が不正なものと，不完全（不正ではないが閉じカッコが足りない）なものがあります．

Part 1

不正な行に関して「構文エラー得点」を計算します．構文エラー得点ってなんやねん．各行の一番左の不正なカッコについて以下の規則で得点を付与し，その合計を回答します．

• ): 3 points.
• ]: 57 points.
• }: 1197 points.
• >: 25137 points.

各行を左から操作します．開きカッコがあればスタックに積み，閉じカッコがあればスタックから下ろします．下ろす際，開きカッコに対応しないのであれば構文エラーで得点が加算されます．

入力が"[{}>"の場合

スタック: []
[{}>

スタック: [ // 開きカッコなのでスタックに積む
[{}>
^ポインタ

スタック: [{ // 開きカッコなのでスタックに積む
[{}>
 ^ポインタ

スタック: [ // "{"を"}"で消費
[{}>
  ^ポインタ

スタック: [ // "["を">"で消費できない！構文エラー，25137ポイント！
[{}>
   ^ポインタ

解答コード

Part 2

不完全な行に対して足りないカッコを補完します．保管する際，以下の規則でやはり「補完ポイント」が得られます（？）．全ての行の補完ポイント中央値を回答します．

得点規則

• 文字を保管する度に
  • いままでの得点を5倍
  • 対応した得点を加算
    • ): 1 point.
    • ]: 2 points.
    • }: 3 points.
    • >: 4 points.

補完処理はPart 1のコードの拡張で実現できます．エラー無く最後の文字まで読んだ時，スタックに残っている開きカッコから閉じカッコを保管します．

入力が"[{"の場合

スタック: []
[{

スタック: [ // 開きカッコなのでスタックに積む
[{
^ポインタ

スタック: [{ // 開きカッコなのでスタックに積む
[{
 ^ポインタ

入力を全て読んだがスタックが空でないので補完可能

スタック: [ // 開きカッコを消費
[{} // 対応する閉じカッコを補完，3ポイント
  ^ポインタ

スタック: // 開きカッコを消費
[{}] // 対応する閉じカッコを補完，15 + 2 = 17ポイント
   ^ポインタ

スタックが空なので修了

解答コード

概要

光るタコのパターンを予測する問題です．

10 * 10のグリッドにタコが隙間なく敷き詰められています（そんなことある？）

• それぞれのタコはエネルギーレベルを持っています．
• レベルは各ステップごとに1増加します
• エネルギーが10以上になるとタコは発光し，エネルギーが即座に0へ戻ります．
  • （つまり，各ステップでタコのエネルギーは0〜9しかありえない）
• 発光した際，周囲8つのタコのエネルギーを1増加します．
• これにより発光の連鎖もあり得ます
  • ただし，そのステップで発光したタコは（エネルギーが0のタコは），ほかのタコによってエネルギーを増加されません．

タコのエネルギーの初期値が次のように与えられます．

5483143223
2745854711
5264556173
6141336146
6357385478
4167524645
2176841721
6882881134
4846848554
5283751526

Part 1

100ステップまでに発光したタコの個数を回答します．

上記の規則を愚直に実装していけば問題ありません．

解答コード

Part 2

全てのタコは同時に発光する瞬間のステップ数を回答します．

これも，Part 1のコードを少し拡張すればすぐに求められます．

解答コード

概要

洞窟を探索します．洞窟はいくつかの部屋にわかれており，次のような形式で地図が入力されます．

start-A
start-b
A-c
A-b
b-d
A-end
b-end

図にすると以下のとおりです．

    start
    /   \
c--A-----b--d
    \   /
     end

部屋には小部屋（小文字で表される）と大部屋（大文字で表される）があります．

Part 1

それぞれの小部屋を高々1度しか訪れてはいけない場合の，スタートからゴールまでのパスの数を回答します．

グラフの表現には様々な方法があります．ハッシュマップや集合が使えればそれが一番楽だと思いますが，しっかりとノード，枝といった構造体を作ってもいいですね．

全てのパスを求めなければなりませんが，計算量が問題となるほどのグラフではありませんでした．そのため，愚直にDFSで解きました．

type Node = String;
type Path = Vec<Node>;
fn visit(path: &Path, map: &Map) -> Vec<Path> {}

として，パスを見ながら行ける部屋に全て行くというものです．

解答コード

Part 2

1度だけ個部屋に2度訪れていい という条件のもとで，スタートからゴールまでのパスの数を回答します．各部屋に2度訪れても良いというわけではないので注意してください．

基本的にはPart 1の拡張で解けます．

解答コード

概要

おりがみをする問題です．潜水艦の赤外線カメラを使用したいのですが，そのカメラを使用するためのシリアルキーが折り紙に印字されているらしいです．

入力は次のようなものです．

6,10
0,14
9,10
0,3
10,4
4,11
6,0
6,12
4,1
0,13
10,12
3,4
3,0
8,4
1,10
2,14
8,10
9,0

fold along y=7
fold along x=5

入力の最初の方には2次元平面の点が並んでいます．この点は透明な折り紙シートに打たれている点です．最後の方には折り方の指示が書かれています．例えば，fold along y=7は $y = 7$ の直線に紙を折ることを示しています．

Part 1

紙を1回折った後の点の数を回答します．

まず，点群の表現方法について考えます．本番用のパズル入力の折り方指示を見ると，x = 655といった大きな数字であることがわかります．つまり，この紙の高さや幅は1300以上もあるということです．紙を2次元配列で表現する方法もありますが，約170万個もの要素をメモリ上に確保するのは大変そうです．そのため，以下のようにガッシュセットを使って点群を表現することにしました．

type Point = (u32, u32);
type Map = HashSet<Point>;

これによって，メモリ消費量が点の数に対して線形になるのでエコだと思います．

次に，紙を折るという処理を考えます．とはいえ座標を変換するだけなので少し考えればかんたんです．例えば以下の紙上の点pを座標変換する場合を考えます．

  01234
0 .....
1 .....
2 .....
3 ----- // y=3で折る
4 .....
5 ..p..
6 .....

ここで，x座標はそのまま2です．y座標に関しては，「折り目からpまでの距離の2倍をpから引けばいい」と図形的にわかります．したがって，

となります．

  01234
0 .....
1 ..p..
2 .....
3 ----- // y=3で折った

解答コード

Part 2

Part 1のコードを使って，残りの指示通りに折っていくとシリアルキーが図形的に浮かび上がります．Mapを表示する関数を追加で実装する必要があるでしょう．

解答コード

概要

ポリマーの生成過程をシミュレートします．次のような入力が与えられます．

NNCB

CH -> B
HH -> N
CB -> H
NH -> C
HB -> C
HC -> B
HN -> C
NN -> C
BH -> H
NC -> B
NB -> B
BN -> B
BB -> N
BC -> B
CC -> N
CN -> C

最初の行はポリマーの初期状態です．ポリマーはB，N，C，Hといった要素が単連結してできています．

その後の入力はポリマーの生成ルールです．AB -> Cといった表記は，1ステップ経過するたびにABの間にCという要素が増えることを意味しています．

ポリマーは以下のように増えていきます．

Template:     NNCB

"NN -> C"によってCを挿入，"NC -> B"によってBを挿入，"CB -> H"によってHを挿入

After step 1: NCNBCHB
After step 2: NBCCNBBBCBHCB
...

Part 1

10ステップ経過後のポリマーにおいて，一番多い要素と一番少ない要素の差を回答します．

ナイーブな解法

以下のように，可変長配列などを用いてポリマーを表現し，先頭から生成ルールを適用していきます．

現状のポリマー：['N',      'N',      'C',      'B']

  次のポリマー：['N', 'C', 'N', 'B', 'C', 'H', 'B']
                       ^追加     ^追加     ^追加
...

しかし，ポリマー長さは二次関数的に増加していくので，この方法ではすぐに限界が来ます．

効率的な解法

上記の手法では，とても長いポリマーに対して高々16個しかない生成ルールを繰り返し適用しているのがムダでした．今回の問題では我々は要素の 隣接 にしか興味がないことに気づきました．そのため，以下のようなアルゴリズムで効率よく解けます．

Template: NNCB
→次の構造を初期化する

// 要素個数マップ
[
    N -> 2
    C -> 1
    B -> 1
]
// 隣接個数マップ
[
    NN -> 1
    NC -> 1
    CB -> 1
]

ステップ1
1. 新しい隣接個数マップを用意
2. 隣接個数マップの各隣接について以下を実行
  1. 新しく増える要素をルールから特定
  2. 新しく増える隣接を，新しい隣接個数マップに追加
  例：NN -> 1の場合
    →ルール「NN->C」によって間にCが増える．
    →つまり「NC」と「CN」の隣接が増えるので，新しい隣接個数マップに記録．

ステップ2
...

解答コード

Part 2

上記のナイーブな実装だと厳しいはずです．効率的な解法を使いました．

解答コード

概要

次のような入力が与えられます．

1163751742
1381373672
2136511328
3694931569
7463417111
1319128137
1359912421
3125421639
1293138521
2311944581

これは2次元のマップで，左上がスタート，左下がゴール，各数値はその地点の リスクレベル です．

Part 1

あるパスのリスクレベルは，その軌跡の各地点のリスクレベルの合計です．スタートからゴールまでのあらゆるパスの中で，もっとも低いリスクレベルの値を回答します．

この問題は普通にA*探索で突破しました．ヒューリスティック関数には，ゴールまでのマンハッタン距離を採用しました．

解答コード

Part 2

Part 1に比べてマップの広さが1辺5倍になります．これもPart 1と全く同じアルゴリズムで解きました．ただし，探索に4分ほどかかってしまっています．こう少し効率的な解き方がありそうです．

解答コード

概要

バイナリにデコードされた数式をパースする問題です．次のような入力が与えられます．

E20D7880532D4E551A5791BD7B8C964C1548CB3...

上記のデータがどのような数式を表すのか…という仕様の部分は問題本文を参照してください．

今までの問題と比べて仕様が複雑です．難しいアルゴリズムなどは必要ない代わりに，仕様を正確にコードで変換するモデリング力が試されます．ときにはテストなども書きつつ，動作を確認しながらコーディングする必要があるでしょう．私はテストを書いていませんが．

Part 1

全てのパケットにはバージョン番号があり，ここではその番号の合計値を回答します．パケットのパースがうまくできているかを一度確かめに来ている感じです．

どうせ後から実際の計算も行わなければならなくなるので，入力データ -[パーサー]-> AST -[評価器]-> 計算結果という構成をとることにしました．

ASTといってもそんなに複雑なものではなくて，以下のようなノードのあつまりです．

enum Node {
    Literal {
        version: u8,
        type_id: u8,
        value: u128,
    },
    Operator {
        version: u8,
        type_id: u8,
        nodes: Vec<Node>,
    },
}

Part 1ではパーサーのみを愚直に実装しました．

解答コード

Part 2

Part 2ではASTを値に評価する部分を作成しました．こちらのほうが分量は軽かったです．

解答コード

概要

簡単な物理シミュレーションを実装します．鍵が海のある領域にあるかもしれないため，そこにセンサーを放り投げて調査するそうです．

調査したい範囲に関する次のような入力が与えられます．

target area: x=20..30, y=-10..-5

ここは2次元空間で，自分は(0, 0)にいます．センサーをSから右上に投げた様子を図示すると次のようになります．

.............#....#............
.......#..............#........
...............................
S........................#.....
...............................
...............................
...........................#...
...............................
....................TTTTTTTTTTT
....................TTTTTTTTTTT
....................TTTTTTTT#TT
....................TTTTTTTTTTT
....................TTTTTTTTTTT
....................TTTTTTTTTTT

放り投げたセンサーは次の法則で運動します．

• 各ステップごとに
  • 横方向の速度が1減少する（水の抵抗）
  • 深さ方向の速度が1増加する（重力加速度）

Part 1

Sから様々な初期速度でセンサーを投げてターゲットに入ったとして，センサーが到達する最も高い位置を回答します．

なお，次のような オーバーシュート は領域に入ったとみなされません．

S..............................................................
...............................................................
...............................................................
...............................................................
.................#.............................................
....................TTTTTTTTTTT................................
....................TTTTTTTTTTT................................
....................TTTTTTTTTTT................................
....................TTTTTTTTTTT................................
....................TTTTTTTTTTT..#.............................
....................TTTTTTTTTTT................................
...............................................................
...............................................................
...............................................................
...............................................................
................................................#..............
...............................................................
...............................................................
...............................................................
...............................................................
...............................................................
...............................................................
..............................................................#

→ 速度が早すぎて領域を飛び越してしまっています．

愚直な解法

あらゆる方向に飛ばしてみる，という方法をまず思いつきます．つまり初速 $\vec{v_0} = (v_x, v_y)$ を $(-10000, -10000)$ 〜 $(10000, 10000)$ くらいまで雑に試してみるというものです．

少し賢い解法

物理を少し知っていれば，ベクトルは分解できることに気づきます．つまり，今回 $v_x$ には興味がないということです．したがって， $(\_, -10000)$ 〜 $(\_, 10000)$ を試せば十分というわけです．私はこの方法で解きました．

賢い解法

もう少し軌道を観察していると，打ち上げたセンサーは $(\_, -v_y)$ で位置 $(\_, 0)$ に落ちてくるのに気づきます．つまり，最も高い高度を目指して初速 $v_y$ を増加させると，その逆の速度で位置0に落下してくるということです．そして，落下速度が早すぎると次のステップで， $v_y + 1$ の落下速度で領域をオーバーシュートしてしまいます．したがって，原点からの落下速度が領域をギリギリオーバーシュートしない打ち上げ速度を狙えばいいということです．

この入力を例に考えてみますと，

target area: x=20..30, y=-10..-5

位置0から下方向に投げたとき，ギリギリ領域に収まる落下速度は-10です．つまりyの下端ギリギリです．したがって，原点での落下速度は −9が最速で，初速も9とできますので，最高高度は $9 + 8 + 7 + \cdots + 2 + 1 = (10 \times 9) / 2 = 45$ となります．

コードすら必要なく解けてしまいますね！

解答コード

Part 2

領域に収まるすべての初速のパターン数を回答します．

私は雑な全域探索で解きました．上記の考察から，y方向の初速 $v_y$ に関しては $\pm{領域の下端位置}$ くらいの範囲を探索すればいいと気づきます．x方向の探索範囲についても1ステップ目でオーバーシュートするような範囲は探索する必要がないため，0〜領域の右端位置くらいまでを探索すればいいでしょう．

解答コード

概要

クサウオが鍵を見たといいます．そして，数学の宿題を手伝ってくれたらどこで見たのか教えてくれるそうです．

クサウオは クサウオ数 という独自の命数法を使っていて，以下のようなものです．

[1,2]
[[1,2],3]
[9,[8,7]]
[[1,9],[8,5]]

クサウオ数は常に2つの要素をもつタプルです．要素には0〜9またはクサウオ数が入ります．

宿題は与えられた全てのクサウオ数の合計を求めることです．以下のようなクサウオ数のリストが入力として与えられます．

[[[0,[4,5]],[0,0]],[[[4,5],[2,6]],[9,5]]]
[7,[[[3,7],[4,3]],[[6,3],[8,8]]]]
[[2,[[0,8],[3,4]]],[[[6,7],1],[7,[1,6]]]]
...

2つのクサウオ数の足し算は以下の手順によって行われます．

1. 2つのクサウオ数を新たなタプルとして連結する
   1. 例：[1,2] + [3,4] = [[1,2],[3,4]]
2. 連結したクサウオ数に 削減処理 を適用する

削減処理は以下のように行われます．

1. (ラベル)
2. 爆発：4回以上ネストされているクサウオ数がある場合，そのような一番左のクサウオ数が 爆発する．(ラベル)に戻る
3. 分裂：10以上の数がある場合，その数は 分裂して 新たなクサウオ数になる．(ラベル)に戻る
4. おわり

爆発は以下のように行われます．

[[6,[5,[4,[3,2]]]],1]
          ^^^^^ 爆発対象（ネストが4以上）

1. クサウオ数が爆発すると，その左右の要素が飛んでいき，一番始めにぶつかった数に加算される
2. 爆発したクサウオ数は0になる

したがって以下のようになります

        v 3を加算  v 2を加算
[[6,[5,[7,  0  ]]],3]
          ^^^^^ 爆発対象（0になった）

なお，加算対象が無い場合は何もしません

数の分裂は[切り捨て(数/2),切り上げ(数/2)]のように行われます．例えば11は[5,6]になります．

以上，仕様が複雑なので注意して実装する必要がありますね．

Part 1

与えられた全てのクサウオ数を足した場合の マグニチュード を回答します．クサウオ数のマグニチュードは $左の数 \times 3 + 右の数 \times 2$ で求められます．

難しいのは，クサウオ数をどのように表現するのか，という点だとおもいます．そのまま実装するのであれば配列やタプルをネストすることになるわけですが，そうすると爆発処理が実装しづらそうです．したがって，次のようなcharの配列を用いることにしました．

[[6,[5,[4,[3,2]]]],1]

上記のクサウオ数は以下のように表す

['[', '[', '6', '[', '5', '[', '4', '[', '3', '2', ']', ']', ']', ']', '1', ']']

こうすることで，爆発の際に現時点から左側の最初の数を特定といった処理も，そのまま配列の走査として書けます．

解答コード

Part 2

与えられたクサウオ数のうち，異なる2つを足し合わせる場合の最大のマグニチュードを回答します．

素直に全ての組み合わせを計算すればOKです．

解答コード

概要

3次元空間で点群のマッチングを行う問題です．簡易的なSLAMといえるかも．

3次元空間の海中にビーコンと，そのスキャナーがいくつか展開されました．スキャナーによるスキャン情報が以下のように与えられます．

--- scanner 0 ---
404,-588,-901
528,-643,409
-838,591,734
...

--- scanner 1 ---
686,422,578
605,423,415
515,917,-361
...

--- scanner 2 ---
649,640,665
682,-795,504
-784,533,-524
...

--- scanner 3 ---
-589,542,597
605,-692,669
-500,565,-823
...

--- scanner 4 ---
727,592,562
-293,-554,779
441,611,-461
...

スキャナーは自分が検知したビーコンの位置を，自分からの相対座標で報告しています．スキャナーのスキャン可能範囲は， $(\pm{1000}, \pm{1000}, \pm{1000})$ です．

すべてのスキャナーが同じ方向を向いているとは限りません．スキャナーは，90度単位で様々な姿勢をとり得ます．$x$，$y$，$z$，$-x$，$-y$，$-z$」に対してそれぞれ4種類の回転が考えられるため，24種類の姿勢があり得ます．

各スキャナーに対して，最小12個のビーコンを共有してスキャンしているスキャナーが1つ以上あります．

Part 1

マップ全体のビーコンの数を回答します．

そのためには，すべてのビーコン群（=スキャン結果）を統合してマップ全体のビーコン群を得る必要があります．

[ビーコン群1] + [ビーコン群2] + [ビーコン群3] + ... = [全てのビーコン群]

つまり，2つのビーコン群をマッチングする，上記の+演算子を実装できれば良いわけです．

スキャナ1と2の2つのビーコン群が与えられて，スキャナ1を基準とした時のスキャナ2の位置と回転を返す，次のような関数を考えました．

use euclid::default::{Point3D, Vector3D};
type Vector = Vector3D<i32>;
type Point = Point3D<i32>;
type Scan = HashSet<Point>;

// (i32, Vector)は，スキャナ1を基準としたスキャナ2の(回転id, 位置)です
// 回転idにか関しては後述します
// なお，マッチしなければNoneを返します
fn match_scan(s1: &Scan, s2: &Scan) -> Option<(i32, Vector)> {
    // ...
}

「2つのビーコン群を統合したビーコン群」が欲しいんじゃないの？ と思われるかもしれません．しかし，結局本質的に必要なのは2つのスキャナの相対位置と回転です．これらがわかればビーコン群の座標変換は自由にできます．むしろマッチングを行った結果何をしたいのかは外部の任せるというほうが，使い勝手が良いかなと思ってこのようにしました．

ここで， スキャナ2のビーコン群をあらゆる姿勢に回転させたうえで，スキャナ1の各ビーコンについて，スキャナ2の各ビーコンと同一だと仮定した上で最低12個の一致があるか調べる ．という処理を思いつきました．自然言語だとうまく言えませんが，疑似コードでは以下のようになります．

for 回転id in 0..24 {
    for ビーコン1 in スキャン結果1 {
        for ビーコン2 in スキャン結果2 {
            // スキャン結果2を回転idで回転
            // スキャン結果1と2で12個以上のビーコンのマッチがあるか調べる
        }
    }
}

…なかなか計算量がヤバそうな処理ですが，ここはRustさんに頑張ってもらいます．もうすこし良い方法がありそうです．

この処理を実装するためには，あるビーコンの座標を24種類の姿勢に回転させる関数が必要になります．そのために，まずは，各軸を中心に座標を回転させる関数を次のように実装しました．

// angle_id: 0 ~ 3
fn rotate_x(p: Point, angle_id: i32) -> Point {
    // ...
}
fn rotate_y(p: Point, angle_id: i32) -> Point {
    // ...
}
fn rotate_z(p: Point, angle_id: i32) -> Point {
    // ...
}

これらの基本的な操作を用いて，24種類の回転をする次のような関数が書けます．

// angle_id: 0 ~ 23
fn rotate(p: Point, angle_id: i32) -> Point {
    // メモ：pがangle_id 1〜23を向いているとして，それをangle_id 0に戻すことをイメージして書いています

    // どの軸に対する姿勢か，0: x, 1: y, 2: z
    let axis_id = angle_id / 8;
    // マイナス方向を向くか，0: 向かない, 1: 向く
    let flip_id = (angle_id / 4) % 2;
    // 軸に対して何回回転するか
    let rotate_angle_id = angle_id % 4;

    let axis_rotated_point = match axis_id {
        // 各軸のほうを向くように回転
    };

    let flipped_point = if flip_id == 0 {
        // なにもしない
    } else {
        match axis_id {
            // 軸の反対側を向くように回転
        }
    };

    match axis_id {
        // 各軸を中心に所定の角度だけ回転
    }
}

以上の処理によりすべてのビーコン群を統合すると，マップ全体のビーコンの数がわかります．

解答コード

Part 2

各スキャナのマンハッタン距離を計算した時，もっとも遠い距離を回答します．

先程の関数を用いてスキャナ0を基準としたすべてのスキャナの絶対位置を求めます．そのうえですべての組み合わせを考慮して最大値を求めれば良いです．

解答コード

概要

バイナリ画像のフィルタ処理をする問題です．次のような入力が与えられます．

..#.#..#####.#.#.#.###.##.....###.##.#..###.####..#####..#....#..#..##..###..######.###...####..#..#####..##..#.#####...##.#.#..#.##..#.#......#.###.######.###.####...#.##.##..#..#..#####.....#.#....###..#.##......#.....#..#..#..##..#...##.######.####.####.#.#...#.......#..#.#.#...####.##.#......#..#...##.#.##..#...##.#.##..###.#......#.#.......#.#.#.####.###.##...#.....####.#..#..#.##.#....##..#.####....##...##..#...#......#.#.......#.......##..####..#...#.#.#...##..#.#..###..#####........#..####......#..#

#..#.
#....
##..#
..#..
..###

上の方は画像処理フィルタ，下の方は入力画像を表しています．

画像処理フィルタの適用規則について，以下の画像の中心のピクセルを処理する場合を例に説明します．

#..#.
#....
##..#
..#..
..###

ここで，処理したいピクセルを中心とする3 * 3の領域を考えます．

# . . # .
#[. . .].
#[# . .]#
.[. # .].
. . # # #

この領域を左上から右下へ順番に読むと...#...#.となります．これを000100010と解釈して10進数になおすと34になります．最終的に，処理したいピクセルは，入力されたフィルタ文字列の34文字目，つまり#に変換されます．

0         10        20        30  34    40        50        60        70
|         |         |         |   |     |         |         |         |
..#.#..#####.#.#.#.###.##.....###.##.#..###.####..#####..#....#..#..##..##

この処理を画像全体のピクセルに適用します．

なお，本問題で扱う画像は無限大の大きさを持つらしいので注意です．入力で与えられる領域外には.のピクセルが広がっています．

Part 1

フィルタを2回適用した後の#の数を回答します．

無限の大きさを持つ画像に対してフィルタを適用するわけですが，実際には入力画像の周辺のピクセルだけを計算し，範囲外のピクセルに関しては一様なのでまとめて管理すれば問題ありません．したがって，マップを次のように定義します．

use rusttype::Point as RPoint;
type Point = RPoint<i32>;
struct Map {
    pub hashset: HashSet<Point>,
    pub min_x: i32,
    pub max_x: i32,
    pub min_y: i32,
    pub max_y: i32,
    pub outside_cell_state: bool,
}

範囲外のピクセルの状態はoutside_cell_stateによって一括で保持しています．

このマップは，フィルタを適用する度に上下左右方向へ1ピクセルぶんだけ拡張する必要があります．マップの上部を例に説明します．

............[範囲外（全て'#'または'.'）]............
______[フィルタ適用によって新しく拡張される領域]____
##...#..##..##...#.[マップの上端].##...#...#..##..##

「フィルタ適用によって新しく拡張される領域」にフィルタを適用した結果は一様にならないのがわかると思います．フィルタの下段（3段目）が既存の領域の情報を参照するからです．その一段上の領域に関してはそのまま一様なので問題ありません．

というわけで，フィルタを適用する処理は次のように書けます．

pub fn apply_filter(map: &Map, filter: &Filter) -> Self {
    let mut new_map = Map::new();

    for y in self.min_y - 1..=self.max_y + 1 {
        for x in self.min_x - 1..=self.max_x + 1 {
            // 各ピクセルに対してフィルタを適用した結果をnew_mapに保持
        }
    }

    // 範囲外のピクセルの状態にフィルタを適用した結果を計算
    new_map.outside_cell_state = if self.outside_cell_state {
        filter[511]
    } else {
        filter[0]
    };

    new_map
}

解答コード

Part 2

フィルタを50回適用した後の#の数を回答します．Part 1のアルゴリズムを使用すれば問題なく解けます．

解答コード

概要

ディラックダイス という特殊なダイスを使ったボードゲームの展開を考える問題です．

ボードゲームでは，ボード，ポーン，サイコロを使用します．

ボードにはプレイヤーの止まれる10個マス目が円形に配置されており，次のようなものです．

// 10の後は1に戻ります
 |---------------------------------------------------------------
 v                                                              |
[1] -> [2] -> [3] -> [4] -> [5] -> [6] -> [7] -> [8] -> [9] -> [10]

プレイヤーの初期位置は以下のように入力として与えられます．

Player 1 starting position: 4
Player 2 starting position: 8

プレイヤーはそれぞれ自分の得点をもちます．ゲーム開始時点では両者0点です．

最初はプレイヤー1のターンからはじめます．

各ターンで，プレイヤーはサイコロを3回振ります．出た目の合計だけポーンを進めて，止まった位置の数字だけ自分の得点を増やします．その後ターンを交代します．

Part 1

以下の条件で，どちらかが勝つまでゲームを進めます． $負けたほうのプレイヤーの得点 \timesサイコロを振った回数$ を回答します．

• 決定論的サイコロ を用います．決定論的サイコロは，1回目に振ったとき1が出て，次に振ったとき2が出て，100回目に振ったとき100，101回目に振るとまた1が出るようなサイコロです．
• 得点が1000になったプレイヤーを勝利とします．

ここでは特に難しいアルゴリズムを考える必要はありません．素直にゲーム内容をコードに落とし込めばよいです．

解答コード

Part 2

以下の条件において，ゲームのすべての分岐パターンを考慮します． 勝利するパターンが多いプレイヤーのパターン数を回答します．

• ディラックダイス を用いてゲームを進行します．ディラックダイスは3面サイコロです．振る度に3つの可能性に世界が分岐します（そのため， ゲームのすべての分岐パターンを考慮 する必要がある…という設定です）
• 得点が21になったプレイヤーを勝利とします．

つまり，次のようなゲームの分岐をすべて考慮して，プレイヤーそれぞれの勝利パターン数をカウントします．

• プレイヤー1がサイコロで1を出す
  • プレイヤー1がサイコロで1を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで2を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで3を出す
    • ...
      • プレイヤー1 or 2が勝利
• プレイヤー1がサイコロで2を出す
  • プレイヤー1がサイコロで1を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで2を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで3を出す
    • ...
      • プレイヤー1 or 2が勝利
• プレイヤー1がサイコロで3を出す
  • プレイヤー1がサイコロで1を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで2を出す
    • ...
      • プレイヤー1 or 2が勝利
  • プレイヤー1がサイコロで3を出す
    • ...
      • プレイヤー1 or 2が勝利

分岐は木構造なので，次のような深さ優先探索が使えます．

// (p1 wins, p2 wins)
type Wins = (u128, u128);
struct PlayerState {
    pub pos: u32, // 1 ~ 10
    pub score: u32,
}
fn calc_wins(
    current_player: PlayerState,
    next_player: PlayerState,
) -> Wins {
    // プレイヤー1が勝利していたら，return (1, 0);
    // プレイヤー2が勝利していたら，return (0, 1);

    let mut current_wins: u128 = 0;
    let mut next_wins: u128 = 0;
    for dice1 in 0..3 {
        for dice2 in 0..3 {
            for dice3 in 0..3 {
                // 残りのステップについてcalc_winsを呼び出す
                // その結果をcurrent_winsとnext_winsに加算
            }
        }
    }

    return (current_wins, next_wins);
}

一方で，上記の実装では計算量が明らかにヤバそうです．雑に予想すると，各ターンでプレイヤーが平均5点を得るとして，21点貯まるのに5回自分のターンが必要で，ゲーム全体では9回のターンが必要です．そうなるとサイコロを27回くらい振ることになります．

したがってゲームのパターン数は約 $3^{27} = 7,625,597,484,987$ となり，13桁のオーダーになります．やばい．

もう少し最適化の余地を考えてみます．すると，各ターンの分岐はサイコロの合計数が同じならば発生しないことがわかります．つまり，あるターンで1，1，3が出た場合と1，3，1が出た場合では，その後のゲーム進行は全く同じだということです．したがって，先程の処理を次のように変更できます．

// (p1 wins, p2 wins)
type Wins = (u128, u128);
struct PlayerState {
    pub pos: u32, // 1 ~ 10
    pub score: u32,
}
fn calc_wins(
    current_player: PlayerState,
    next_player: PlayerState,
) -> Wins {
    // プレイヤー1が勝利していたら，return (1, 0);
    // プレイヤー2が勝利していたら，return (1, 0);

    let mut current_wins: u128 = 0;
    let mut next_wins: u128 = 0;
    for (roll, freq) in vec![(3, 1), (4, 3), (5, 6), (6, 7), (7, 6), (8, 3), (9, 1)] {
        // 残りのステップについてcalc_winsを呼び出す
        // その結果 * freqを，current_winsとnext_winsに加算
    }

    return (current_wins, next_wins);
}

先ほどと同じようにパターン数を見積もってみますと， $7^{10} = 282,475,249$ となりますので，13桁 -> 9桁オーダーへダイエットに成功しました．

上記の発想を更に一般化すると，ゲームの状態が決定すれば，そこから先の展開もすべて決定的である ということに気づきます．

言い換えれば，calc_winsは純粋関数で，入力が決まれば出力も決まるということです．したがって，この関数の入力と出力のペアをメモしておけば，次回同じ引数で関数を呼び出さずとも出力がわかるという，メモ化による最適化が使えます．

// (p1 wins, p2 wins)
type Wins = (u128, u128);
struct PlayerState {
    pub pos: u32, // 1 ~ 10
    pub score: u32,
}
type GameState = (PlayerState, PlayerState);
type CalcWinsCache = HashMap<GameState, Wins>;
fn calc_wins(
    current_player: PlayerState,
    next_player: PlayerState,
    cahce: &mut CalcWinsCache,
) -> Wins {
    // キャッシュがあればキャッシュからWinsを返す
    // プレイヤー1が勝利していたら，return (1, 0);
    // プレイヤー2が勝利していたら，return (1, 0);

    let mut current_wins: u128 = 0;
    let mut next_wins: u128 = 0;
    for (roll, freq) in vec![(3, 1), (4, 3), (5, 6), (6, 7), (7, 6), (8, 3), (9, 1)] {
        // 残りのステップについてcalc_winsを呼び出す
        // その結果 * freqを，current_winsとnext_winsに加算
    }

    // キャッシュに自分の入力と出力をメモする
    return (current_wins, next_wins);
}

上記の2つの最適化によって，この問題は200msくらいで解けます．勝利数を倍の42にしても1秒くらいで解けてしまいます．57にしたらu128をオーバフローして落ちました．

解答コード

概要

3次元空間の各位置にあるスイッチ（問題文では「炉心」と表現されている）をオン / オフする問題です．

座標が整数の3次元空間上に，全て状態がオフのスイッチが並んでいます．次のような操作手順が入力として与えられます．

on x=-5..47,y=-31..22,z=-19..33
on x=-44..5,y=-27..21,z=-14..35
on x=-49..-1,y=-11..42,z=-10..38
on x=-20..34,y=-40..6,z=-44..1
off x=26..39,y=40..50,z=-2..11
on x=-41..5,y=-41..6,z=-36..8
...

on x=-5..47,y=-31..22,z=-19..33はx=-5..47,y=-31..22,z=-19..33の範囲のスイッチをすべてオンにすることを示しています．off x=26..39,y=40..50,z=-2..11はx=26..39,y=40..50,z=-2..11の範囲のスイッチをすべてオフにすることを示しています．

Part 1

入力の指示を全て実行した場合，x=-50..50,y=-50..50,z=-50..50の範囲でオンになっているスイッチの数を回答します．

扱わなければならない範囲が小さいので，愚直に実装すれば解けます．

解答コード

Part 2

入力の指示を全て実行したあとオンになっているスイッチの数を回答します．

Part 1と違い，考慮しなければならない範囲が膨大なため効率の良いアルゴリズムを考える必要があります．

問題を単純化して考えるために，空間が2次元であり，操作は"on"だけの場合を想定してみます．すると，"on"という操作は， $自身の領域 - 既存の領域との共通部分$ の数だけスイッチをオンにしていることがわかります．

  ↓既存の領域A
+-----------+
|       +---+-------+
|   +---+---+---+   |
|   |(a)|(b)|(c)|   |
*---+---+---+   |   |
    |   +-------+---+
    |    (d)    | ↑既存の領域B
    +-----------+
        ↑新しくonする領域

「(d) = 新しくonする領域 - (a) - (b) - (c)」の数だけスイッチをオンしている

したがって， 既存の領域のOR部分 と 新しくonする領域 のAND部分の面積が知れれば良いわけです．

まず，2つの領域の場合，AND部分の矩形は簡単に求まります．2つの領域をそれぞれ $b_1 = ((b_{11x}, b_{11y}), (b_{12x}, b_{12y}))$ ， $b_2 = ((b_{21x}, b_{21y}), (b_{22x}, b_{22y}))$ とすると，AND部分は，

となります．

次に，「 複数の領域のOR部分 と 単一領域 のAND部分」の面積を求める方法を考えます．結論から言ってしまうと，次のようなコードで実現できます．

fn AND領域の面積を計算(複数領域, 単一領域) -> i32 {
    let mut 面積 = 0;
    for (複数領域要素, index) in 複数領域 {
        面積 += (単一領域 & 複数領域要素).面積
                - AND領域の面積を計算(複数領域[index+1..], (単一領域 & 複数領域要素))
    }
    return 面積
}

このコードの動作を先程の図で説明します．

  ↓既存の領域A
+-----------+
|       +---+-------+
|   +---+---+---+   |
|   |(a)|(b)|(c)|   |
*---+---+---+   |   |
    |   +-------+---+
    |    (d)    | ↑既存の領域B
    +-----------+
        ↑新しくonする領域

「(d) = 新しくonする領域 - (a) - (b) - (c)」の数だけスイッチをオンしている

まず，複数領域要素に既存の領域Aが来た場合，面積には既存の領域A & 新しくonする領域 - ((既存の領域A & 新しくonする領域) & 既存の領域B) = (a)の面積が加算されます．

次に，複数領域要素に既存の領域Bが来た場合，面積には新しくonする領域 & 既存の領域 = (b) + (c)の面積が加算されます．しっかりとAND領域の面積を計算できています．

以上により"on"操作に関しては実装できそうです．次に"off"操作に関して考えていきますが，これまた結論からいいますと以下のようなコードでうまく行きます．

let 面積 = 0;
let 既存領域の集合 = [];
for (モード, 領域) in 入力指示.逆() {
    if モード == "on" {
        aria += 領域.面積() - AND領域の面積を計算(既存領域の集合, 領域);
    }

    既存領域の集合.push(領域);
}

「なんで指示を逆に実行してんねん」 や 「offの時面積いじらないんかい」 などと思われるかもしれません．私なりに理解した結果「"ボタンをoffにする"という操作の結果引かれるべき面積を，それ以前のon操作の処理に引かせている」のだと思いました．

指示1: 領域1をon  // 既存領域に領域3が含まれているので，その領域を自身から除外した部分を面積に足す
指示2: 領域2をon  // 既存領域に領域3が含まれているので，その領域を自身から除外した部分を面積に足す
指示3: 領域3をoff // 面積はいじらないが，既存領域に自身を追加する
指示4: 領域4をon  // ↑に実行していく

以上，上記の処理を3次元に拡張すれば問題が解けます．

解答コード

概要

端脚類（以降"アイテム"）を正しい部屋に移動させる問題です．

次のようなマップとアイテムの初期状態が与えられます．

#############
#...........#
###B#C#B#D###
  #A#D#C#A#
  #########

アイテムはマップ内を以下の条件を守って自由に移動できます．

• あるアイテムが部屋の入口の廊下にとどまったままで，他のアイテムは移動できません
• 別のアイテムが既に入っている部屋には入れません

マップの見方は以下のとおりです．

'#'は壁，'.'はそこに何もないことを表す
'v'の廊下の位置にはアイテムはとどまれない

   v v v v
#############
#...........#  <廊下
###B#C#B#D###  <部屋1
  #A#D#C#A#    <部屋2
  #########

ゴール（整列）状態
#############
#...........#
###A#B#C#D###
  #A#B#C#D#
  #########

各アイテムは1つの位置を動くたびに次のエネルギーを消費します．

• A: 1
• B: 10
• C: 100
• D: 1000

Part 1

アイテムを整列させるために必要な最小エネルギーを回答します．

基本的には各マップの状態をノードとして，DFSやBFSを実行すれば解けます．

しかし，素直に全ての状態を探索すると時間がかかりそうです．アイテムがとどまれる場所は15箇所ありますので，可能な盤面は $15*14*13*12*11*10*9*8 \div 2^4 = 16,216,200$ パターンということになります．ちょっと多くてイヤですね．

今回は以下のような枝切りによって探索時間の短縮を図ります．あるマップの状態から，次に探索すべき状態を生成するget_next_maps関数を考えます．

fn get_next_maps(map: Map) -> Map[] {
    // 正しい位置に入れられるitemがあればいれる
    // →正しい位置に入れられるアイテムがあるのにそれを無視するような不要な操作を枝切り
    for アイテム in 廊下 {
        if アイテムを正しい部屋に入れられる {
            return [アイテムを入れた状態のMap]
        }
    }

    // 取り出せるitemがあればあらゆる位置に取り出す
    // →正しい位置に入れられるアイテムがない
    // →したがって，部屋からいずれかのアイテムを取り出して状況を変えるしか無い
    // →逆に言えば，そのような状況でアイテムを部屋から取り出さないような不要な操作を枝切り
    let 次のMap = []
    for アイテム in 各部屋の移動できるアイテム {
        for 取り出し場所inアイテムを取り出し可能な廊下の位置 {
            次のMap.push(アイテムを取り出し場所に取り出したマップ)
        }
    }
    return 次のMap
}

以上の仕組みを実装することで，現実的な時間内で問題が解けます．

解答コード

Part 2

部屋の深さが2倍の4になります．Part 1のアルゴリズムによって問題なく解けます．

解答コード

概要

独自の処理系上で動作するモデル番号検証プログラムがあります．そのプログラムが受け付けるモデル番号を探索する問題です．

潜水艦のALU：arithmetic logic unitが壊れました．そのため，このALUの代わりとなるものを作成しなければなりません．また，代わりのALUを潜水艦に設置する際，ALU上でモデル番号の検証プログラムが実行され，検証に成功しないとALUは起動しません．有効なモデル番号を見つける必要があります．

モデル番号は14桁の数値です．各桁は1〜9です．0は現れません．

ALUの仕様は以下のとおりです．

• 4つのレジスタを持っています
  • x，y，z，wのレジスタがあります
  • レジスタは整数を保持します
  • プログラム開始前に，レジスタは0に初期化されます．
• 入力メモリをもちます．複数の整数を保持する配列のようなものです．
• 次の命令を解釈できます
  • imp a：入力メモリを1つ消費して，値をaに読み込みます．
  • add a b：aとbの和をaにセットします
  • mul a b：aとbの積をaにセットします
  • div a b：aとbの商をaにセットします
  • mod a b：aとbの剰余をaにセットします
  • eql a b：aとbが等しい場合は1を，等しくない場合は0をaにセットします
• ジャンプ命令はありません

MONAD：MOdel Number Automatic Detector program（モデル番号検証プログラム）が次のような入力として与えられます．

inp w
mul x 0
add x z
mod x 26
div z 1
add x 11
eql x w
eql x 0
mul y 0
...

MONADはinp命令によってモデル番号の各桁を左から読み取ります．例えば，モデル番号が1234...の場合，最初のimp a命令は1をaにセットします．次のimp a命令は2をaにセットします．

有効なモデル番号に対してMONADのすべてのステップを実行するとzは0になります．無効なモデル番号に対して実行するとzは0以外になります．

Part 1

MONADが受け付ける最大のモデル番号を回答します．

はじめにMONADの挙動を観察して作戦を立ててから実装に入っていきたいと思います．

観察

なにはともあれMONADをRustで実装してみたいと思います．MONADのアルゴリズムで最終的なzを計算する関数をorig_calc_zとしました．名前がひどいのは許してください．

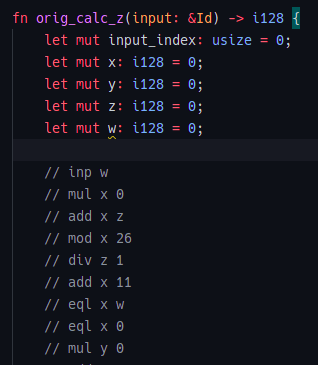
次のように関数を宣言して，

fn orig_calc_z(input: &Id) -> i128 {
    let mut input_index: usize = 0;
    let mut x: i128 = 0;
    let mut y: i128 = 0;
    let mut z: i128 = 0;
    let mut w: i128 = 0;
}

おもむろにMONADのコードをコメントとして貼り付けます．

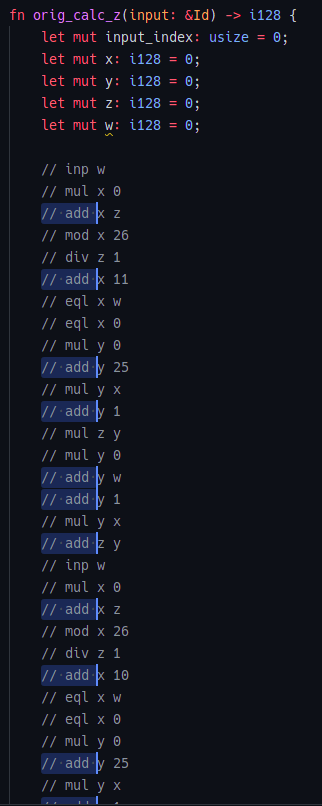
ここで，// add をマルチカーソルで選択して…

コピペを駆使すれば…

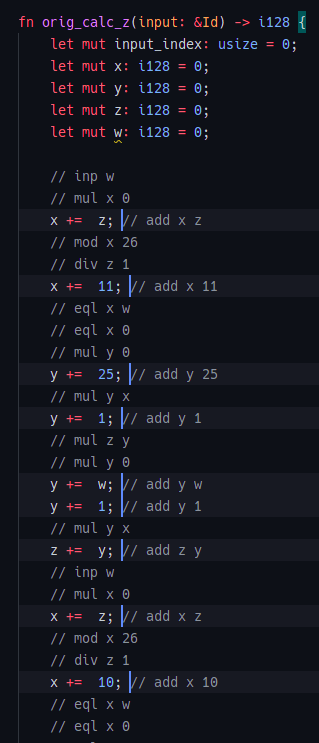
add命令の実装完了です！他の命令に関しても同様に実装していき，MONADが動くようになりました．

fn orig_calc_z(input: &Id) -> i128 {
    let mut input_index: usize = 0;
    let mut x: i128 = 0;
    let mut y: i128 = 0;
    let mut z: i128 = 0;
    let mut w: i128 = 0;

    w = input[input_index]; //inp w
    x *= 0; //mul x 0
    x += z; //add x z
    x %= 26; //mod x 26
    z /= 1; //div z 1
    x += 11; //add x 11
    x = eql(x, w); //eql x w
    x = eql(x, 0); //eql x 0
    y *= 0; //mul y 0
    ...

手始めに，これを使って全域探索してみました．99999999999999からモデル番号をデクリメントしつつ探索したのですが，運良くヒットする…ということはありませんでした．やはりパターン数が多すぎます．

より効率的に探索するためには，MONADの処理に関してさらに理解する必要がありそうです．そこで，いったんMONADを自分なりの数式に落とし込んで再実装してみることにしました．また，処理を数式で表すことで，あわよくば解を代数的に求められないかな〜という思惑もありました．これは失敗でしたが．

数式化によって一定の法則が見えまして，次のような独自のMONADを作ることができました．

fn calc_z(input: &Id) -> i128 {
    let A = [1, 1, 1, 26, 1, 1, 1, 26, 26, 1, 26, 26, 26, 26];
    let B = [11, 10, 13, -10, 11, 11, 12, -11, -7, 13, -13, 0, -11, 0];
    let C = [1, 10, 2, 5, 6, 0, 16, 12, 15, 7, 6, 5, 6, 15];

    let mut z = [0; INPUT_DIGITS_NUM];
    for i in 0..INPUT_DIGITS_NUM {
        let prev_z = if i == 0 { 0 } else { z[i - 1] };
        let x = (prev_z % 26) + B[i] != input[i];
        z[i] = (prev_z / A[i]) * if x { 26 } else { 1 } + if x { input[i] + C[i] } else { 0 };
    }

    z[13]
}

#[cfg(test)]
mod tests {
    use crate::{calc_z, int2id, orig_calc_z};

    #[test]
    fn test_calc_z() {
        let mut num = 0;
        for _ in 0..10000 {
            let input = int2id(num);
            assert_eq!(orig_calc_z(&input), calc_z(&input));

            println!("{:?}", input);

            num += (9 as u128).pow(5);
        }
    }
}

テストも書きました，10000個のモデル番号に対する計算結果が，オリジナルのMONADと独自のMONADで一致することも確かめました．

ここまでの観察で，MONADの本質的な部分は，inputの個数だけzを更新する部分であることがわかりました．

fn calc_z(input: &Id) -> i128 {
    // よくわからん定数

    let mut z = [0; INPUT_DIGITS_NUM];
    for i in 0..INPUT_DIGITS_NUM {
        // よくわからん処理
        z[i] = // よくわからん式 (a)
    }

    z[13]
}

また，zの配列を表示してみると，多くのモデル番号ではzの値が大きなものに発散しているようでした．したがって，今回の問題ではzをいかに発散させずに0へ持っていけるかが重要となりそうです．

上記のzの更新式(a)を見てみます．

z[i] = (prev_z / A[i]) * if x { 26 } else { 1 }
       + if x { input[i] + C[i] } else { 0 };

zを増加させる項である* if x { 26 } else { 1 }と+ if x { input[i] + C[i] } else { 0 }に着目します．どちらの項も，xという謎の真偽値がtureの時にzを増加させ，そうでない場合は値を変化させないことがわかります．

一方で，zを減少させる可能性があるのはprev_z / A[i]の部分だけです．ここでAは次のような定数です．

let A = [1, 1, 1, 26, 1, 1, 1, 26, 26, 1, 26, 26, 26, 26];

つまり，モデル番号によらず，zは26で7回割られます．一方で，* if x { 26 } else { 1 }を思い出すと，xがtrueの場合はせっかく減少したzを打ち消してしまうことに気づきます．また， どのような1桁目のモデル番号を与えても最初のxはtrue．つまり z[0]は0より大きい ということも確かめました．

したがって， 最初のtrueを除いて，xが7回以上trueになった時点で，そのモデル番号は無効．つまり xが8回以上trueとなった時点で，そのモデル番号は無効 といえるので，この条件で枝切りができそうです．

+ if x { input[i] + C[i] } else { 0 }とかいう項が釈然としませんが，とりあえず無視します．

実装

各桁におけるzの計算をノードとして，深さ優先探索で解きました．ただし，xがtrueとなった回数を数えておき，それが8回以上となった場合枝切りします．

struct SearchState {
    digit_index: usize,
    prev_z: i128,
    true_x_num: i32,
    show_progress: bool,
}
fn search_id(state: SearchState) -> Option<Id> {
    // 最終桁までステップを終えていて，かつzが0ならモデル番号を返す

    // 枝切り
    if state.true_x_num >= 8 {
        return None;
    }

    // 現在の桁を9〜1まで試す
    for digit in (1..=9).rev() {
        let z = // zを計算

        // 次の桁に対して自分自身を呼び出す
    }

    None
}

上記のアルゴリズムによって，およそ800msくらいで解が求まりました．

解答コード

Part 2

MONADが受け付ける最小のモデル番号を回答します．

Part 1のコードを少し改変すれば解けます．

解答コード

概要

ナマコの動きを予想する問題です．

海底（2次元空間）にナマコが大量にいます（こわい）．潜水艦を海底のナマコが居ない部分へ安全に着陸させるために，ナマコの動きを計算します．

ナマコの初期状態が次のように与えられます．

v...>>.vv>
.vv>>.vv..
>>.>v>...v
>>v>>.>.v.
v>v.vv.v..
>.>>..v...
.vv..>.>v.
v.v..>>v.v
....v..v.>

.の場所にはナマコはいません．>は東向きのナマコで，右に動きます．vは南向きのナマコで，下に動きます．

ナマコは，次に動くべき場所に空きスペースがあれば動きます．なければ動きません．

マップの上下左右は，それぞれ反対側とつながっています．

Part 1

ナマコを動かしていくと，いずれお互いを邪魔しあってマップに変化がなくなります．ナマコが動かなくなる最初のステップ数を回答します．

ここまでの問題が解けたなら，特に難しいことはありません．素直に実装すれば良いです．

解答コード

Part 2

これまでの問題全てを解いていれば自動的にクリアとなります．

初めてAdvent of Codeというものに参加してみて，本当に辛かったです．後半の問題の難しさと，年末の仕事納めの忙しさのダブルパンチにより，「もうやめちゃおうかな…」と何度も思いました．しかしその分，全ての問題が終わった時の達成感は何ものにも代えがたいものでした．

今回のイベントを通して，合計3000行くらいのRustのコードを書きました．イベントに参加する前は 「ちょっとしたパズルを25問解くだけでしょ」 と思っていましたが，終わってみれば，やっぱりなかなかの分量があるなぁと思います．

前回の記事ではノリでRustに入門しました．今回のイベントによって入門者 -> 初心者くらいまでレベルアップできたのではないかと思っています．日を追うごとに問題が難しくなっていくので，何かの言語の入門に適したイベントではないかと感じました．

最後に，私をAdvent of Code 2021に誘ってくださった @yosuke_furukawa さんにお礼を申し上げます．furukawaさんに誘われるまではこのようなイベントがあることすら知りませんでしたし，多分一人では参加しなかったと思います．イベント中は，お互いのリポジトリへのPushがSlackで通知されるようにしていたのですが，お互いのコミットによってプレッシャーを与えあっていたおかげで，なんとか完走できました．