SICPの備忘録

2023/07/29

これはSICPの読書ノートであり備忘録です。SICPを読む上で私が重要だと感じた単語、読んで理解、解釈したことを記録し、あとで簡単に振り返られるようにします。

また、SICPの簡単な要約としても読めるようにしたいと思います。ただし、基本的に私なりの解釈で書いていますので、もし間違っていたらご指摘ください。

感想文は別に書きました。

1 手続きを用いた抽象化の構築

この本では計算プロセスを学びます。プロセスとは計算過程のことです。プロセスはデータを操作します。プロセスはプログラム（計画）にしたがって計算を進めていきます。プログラムを記述する言語はプログラミング言語と呼ばれます。

この本では、Lispの方言であるSchemeというプログラミング言語を使用します。なぜなら、Lispが持つ特徴がこれからの学習にとても都合が良いからです。その中でも最も重要なのは、Lispで書かれたプロセスが、それ自体データでもあり操作可能だということです。（これは4章で特に強く実感することになります）

1.1 プログラミングの要素

プログラミングの2大要素は、手続きとデータです。手続きは、言語によって記述されたプロセスです。データは、私達が操作したい物です。

1.1.1 式

123や”hello”は、基本的な式です。

+や*は、基本的な手続きです。

式を組み合わせると複合式になります。(+ 1 2 3)は複合式です。一番左の要素+は演算子と呼ばれます。その他の要素は被演算子と呼ばれます。演算子（手続き）を被演算子に適用する、という言い方もします。

(+ 1 2 3)は、評価（evaluation）されると6になります。

1.1.4 複合手続き

複合手続きは、複数の手続きによって構成される手続きです。これは抽象化のテクニックで、プログラムの複雑さを軽減するのに役立ちます。

例えば、(define (square x) (* x x))は、基本手続き*によって構成される複合手続きsquareを作成します。squareによって更に複合手続きを作ることもできます。

特殊形式とは、適用の評価規則以外によって評価される文法形式のことを言います。defineの評価は適用規則を使わないので、defineは特殊形式です。(define (square x) (* x x))は「defineを(square x)と(* x x)に適用する」という意味ではないからです。

1.1.5 手続き適用の置換モデル

手続きの適用がどのように起こるかを考えるために以下のような置換モデルを導入します。

複合手続きを引数に適用するには、手続きの本体に出てくる仮引数を対応する引数で置き換えて、それを評価する。

出典：SICP 非公式日本語版翻訳改訂版、以降同じものについて出典略

例えば、(square 2)は(* 2 2)に置換されます。

しかし、置換モデルはSchemeインタプリタの正確な動作を表してはいません。このあとの章では、このモデルを更に進化させていきます。しかし、現段階ではこれで十分です。

また、適用順序と正規順序について学びます。適用順序では、インタプリタは演算子と被演算子をすべて評価してから、演算子を被演算子に適用します。正規順序では、インタプリタは被演算子の値が必要になるまでそれを評価しません。つまり、演算子を評価し、被演算子を評価せずに演算子を適用します。被演算子は、基本的な手続き（足し算や標準出力への表示など）で必要になったときに、はじめて評価されます。

Lispは適用順序を採用しています。正規順序は、置換モデルを超える範囲では複雑になるからです。一方で、あとの章で登場する無限ストリームが自然に記述できるなどといった利点もあります。

1.1.7 例: ニュートン法による平⽅根

数学では普通、宣⾔的な (何であるか) 記述が関⼼の対象ですが、コンピュータサイエンスでは普通、命令的な（どうやるか）記述が関⼼の対象です。

例えば、2の平方根を計算したいとします。数学では、「 $x$ の平方根 $y$ とは、 $0 \leqq y$ かつ $y^2 = x$ であるようなもの」と宣言的知識として定義されます。

一方で、プログラムで実際に平方根を計算するには、2分法やニュートン法などの命令的知識（手続き的知識とも）が必要になります。

1.2 手続きとそれが⽣成するプロセス

プロセスが手続きによってどのように生成され、変化していくのかを学びます。

1.2.1 線形再帰と反復

自分自身を呼び出す手続きを再帰手続きといいます。

プロセスには形があります。プロセスは、その形によって再帰プロセスと反復プロセスに分けられます。

再帰プロセスは山なりの形になります。以下は再帰プロセスを生成する手続きと、そのプロセスです。

(define
  (factorial n)
  (if (= n 1)
    1
    (* n (factorial (- n 1)))
  )
)

(factorial 6)
(* 6 (factorial 5))
(* 6 (* 5 (factorial 4)))
(* 6 (* 5 (* 4 (factorial 3))))
(* 6 (* 5 (* 4 (* 3 (factorial 2)))))
(* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1))))))
(* 6 (* 5 (* 4 (* 3 (* 2 1)))))
(* 6 (* 5 (* 4 (* 3 2))))
(* 6 (* 5 (* 4 6)))
(* 6 (* 5 24))
(* 6 120)
720

線形プロセスは平らな形になります。以下は再帰プロセスを生成する手続きと、そのプロセスです。

(define
  (factorial n)
  (fact-iter 1 1 n)
)
(define
  (fact-iter product counter max-count)
  (if (> counter max-count)
    product
    (fact-iter
 	 (* counter product)
 	 (+ counter 1)
 	 max-count
    )
  )
)

(factorial 6)
(fact-iter 1 1 6)
(fact-iter 1 2 6)
(fact-iter 2 3 6)
(fact-iter 6 4 6)
(fact-iter 24 5 6)
(fact-iter 120 6 6)
(fact-iter 720 7 6)
720

再帰プロセスでは、呼び出し回数が増加すると必要なメモリも増加します。手続きは、(factorial (- n 1))を計算した後で、それにnを掛けます。つまり、各再帰呼び出しの際に、インタプリタは後で実行する計算（継続）を何らかの方法で覚えておく必要があるということです。

一方、反復プロセスでは、呼び出し回数が増加しても必要なメモリは、少なくともSchemeでは増加しません。計算を進めていく上で、インタプリタはproduct、counter、max-countの3変数を覚えておくだけで十分です。fact-iterの呼び出しが、fact-iterの最後（末尾）の処理であることにも注目します。ここには後で実行すべき計算がありません。したがって、各再帰呼び出しの際に、インタプリタが追加で覚えておくべき情報もありません。

しかし、一般的な言語のほとんどの実装では、手続きが原理的に反復プロセスであっても、呼び出し回数に応じたメモリが必要になります。一般的な言語について、本文ではAdaやPascal、C⾔語を例に挙げています。したがって、これらの言語で反復手続きを記述するには、そのための専用の構文（do、repeat、until、for、whileなど）に頼る場合があります。

反復プロセスを固定の空間で実行できるという性質は、末尾再帰（tail-recursive）や、末尾呼び出しの最適化とも呼ばれます。Schemeは言語仕様として末尾再帰であることを要求しているため、反復のための専用構文は必要ないか、シンタックスシュガー程度で十分です。

プロセスの形（再帰プロセス、反復プロセス）と、再帰手続きという概念を混同しないように気をつけます。前述した2つ階乗計算は、どちらも再帰手続きです。これは、factorialおよびfact-iterが自分自身を呼び出すという構文的特徴によります。しかし、それらが生成するプロセスの形は全く異なります。

1.2.3 増加オーダー

問題の⼤きさを測るパラメータを n として、⼤きさ n の問題についてプロセスが必要とするリソースの量をR(n)とします。

例えば、 $n!$ の階乗計算であれば、 $n$ がパラメータとして適切でしょう。

$Θ$ （シータ）記法は、 $n$ に対するリソース $R(n)$ の増加の程度を表す記法で、以下のようなものです。

任意の⼗分に⼤きなnに対して、nと独⽴な正の定数k1とk2が存在し、 $k1 f(n) \leq R(n) \leq k2 f(n)$ を満たすとき、R(n)は増加オーダーがΘ(f(n))であると⾔い、 $R(n) = Θ(f(n))$ （シータf(n)と読む）と書きます。

（別の⾔い⽅をすると、⼤きなnに対して、R(n)の値はk1 f(n)とk2 f(n)で挟まれるということです）

補足：他に $O$ （ビッグオー）記法というのもあります。これは $Θ$ 記法とは別物です。 $R(n) = Θ(f(n))$ は、 $R(n)$ を $f(n)$ の定数倍で上下からはさみます。一方で、 $R(n) = O(f(n))$ は、 $R(n)$ を $f(n)$ の定数倍で上からしか抑えません。私見ですが、世間的には $O$ 記法が有名で、 $Θ$ 記法の意味で $O$ 記法が用いられていることも多いため、2つを混同しないように注意します。（実際に私は混同していました）

1.3 ⾼階手続きによる抽象の定式化

高階手続きは、手続きを操作する手続きです。これは抽象化のテクニックの1つです。

1.3.1 引数としての手続き

手続きは引数として渡せます。

例えば、以下のdouble手続きはprocを引数として受け取り、argに2回適用します。

(define
  (double proc arg)
  (proc (proc arg))
)

(define
  (inc arg)
  (+ arg 1)
)

(double inc 1)
; 3

1.3.2 lambda を使って手続きを構築する

lambdaを使用すると、手続きをその場で作れます。特に名前をつけるまでもない手続きを定義する場合に便利です。

(define
  (double proc arg)
  (proc (proc arg))
)

(double (lambda (arg) (+ arg 1)) 1)
; 3

2が数値のリテラル、”abc”が文字列のリテラルであるのと同じように、lambdaは手続きのリテラルです。したがって次のように書けます。

(define one 1)
one
; 1

(define inc (lambda (arg) (+ arg 1)))
(inc 1)
; 2

1.3.4 返り値としての手続き

手続きは、返り値として返すこともできます。例えば以下のようにできます。

(define (make-plus-n n) (lambda (arg) (+ arg n)))

(define plus-two (make-plus-n 2))
(plus-two 1)
; 3
(plus-two 2)
; 4
(plus-two 3)
; 5

抽象化とファーストクラス手続き

⼀般的に、プログラミング⾔語は計算要素の操作⽅法に制約を課すものです。制約が最も少ない要素は、「ファーストクラス (first-class、または第一級) の地位を持つ」と言います。

ファーストクラスの要素は、（制約が少ないため）例えば以下のようなことができます。

変数によって名前をつけることができる。

手続きに引数として渡すことができる。

手続きの返り値になることができる。

データ構造に組み込むことができる。

Lispにおいて手続きはファーストクラスです。

2 データを用いた抽象化の構築

複合データは、複数のデータの組み合わせです。

2.1 データ抽象化⼊⾨

Lispにはペアという複合構造があります。ペアは2つのデータの順序対です。

cons、car、cdrはペアに関する基本手続きです。consはペアを生成します。carはペアの1つ目のデータを取り出します。cdrはペアの2つ目のデータを取り出します。

データ抽象化は、抽象化のテクニックです。データ抽象化は、複合データがどのように構築されるかということを、その利用者から隠蔽します。

コンストラクタは複合データを作成する手続きです。例えば有理数を複合データと表す場合は以下のようになります。

(define (make-rat n d) (cons n d))

セレクタは複合データからデータを取り出す手続きです。有理数のセレクタは以下のようになります。

(define (numer x) (car x))
(define (denom x) (cdr x))

consはペアのコンストラクタ、carとcdrはペアのセレクタです。

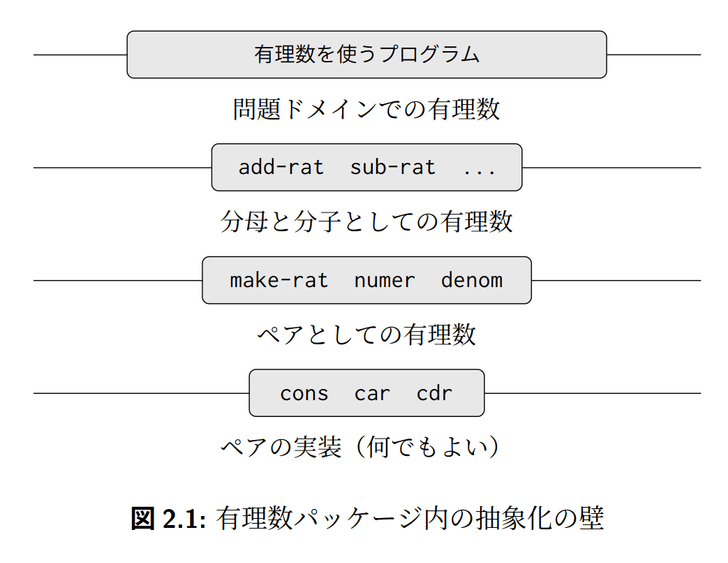
2.1.2 抽象化の壁

例えば、有理数の加算手続きは、make-rat、numer、denomだけで作成できます。加算手続きの作者は、有理数の複合データオブジェクトの構成方法や、cons、car、cdrについては何も知らなくて良いことに注目します。

また、有理数を使って数学の宿題を解きたいとします。その場合、有理数の加算、減算、乗算、除算などの手続きだけでプログラムを書けるはずです。ここで、加算や減算が内部でどのように行われているのかを知る必要はありません。

振り返ると、私達がmake-ratを作成したとき、consによってペアがSchemeの内部でどのように実現されているのかを知る必要はありませんでした。

このように、コンストラクタとセレクタによって抽象化の壁ができていることに注目します。抽象化の壁は、異なる抽象レベルをつなぐためのインターフェースです。

抽象化の壁により、複雑性が隠蔽されます。詳細の実装を後回しにして抽象的な設計に集中できます。各レベルの手続きは、1つ下のレベルの壁（インターフェース）に依存しています。したがって、あとから詳細の実装を変えたくなったとしても、（インターフェースを変更しない限り）修正は壁の内側だけで済みます。

2.1.3 データとは何か

データとは、「コンストラクタ、セレクタ、満たさなければならない条件」によって定義されるものです。

例えばペアの場合、コンストラクタはcons、セレクタはcarとcdr、満たさなければならない条件は以下の2つです。

(car (cons a b))はaを返す
(cdr (cons a b))はbを返す

このような性質を持つものなら、それがどのような詳細な実装を隠蔽していたとしても「ペア」データとして見えるでしょう。

例えば、手続きだけでペアを実装する方法があります。

(define (cons x y) (lambda (m) (m x y)))
(define (car z) (z (lambda (p q) p)))
(define (cdr z) (z (lambda (p q) q)))

cons、car、cdrを使う限り、ペアの利用者は、ここで定義されているペアと、Schemeが用意している本物のペアを区別できません。どちらも同じように振る舞い、問題なく利用できます。

2.2.1 列の表現

列（sequence）は、データの順序付き集合です。

リスト（list）は列の一種で、ペアによって構成されます。

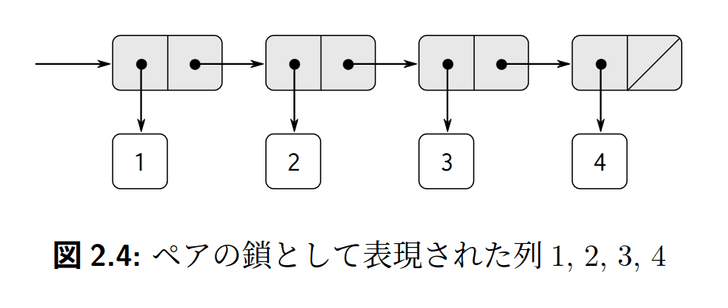
例えば、1、2、3、4というリストは以下のように構成できます。

(cons 1 (cons 2 (cons 3 (cons 4 null))))

nullまたはnilはリストを終端します。または、空リストと考えることもできます。一般に、リストの先頭にhogeデータを追加するときは(cons hoge list)とします。ここで(cons hoge null)は、hogeのみを要素とする長さ1のリストになります。したがって、nullは空のリストであったと考えるのが自然です。

リストの構造を「箱とポインタ表現」で表すと次のようになります。

2.3 記号データ

クォート（quote）は、データオブジェクトそのものを表現するための特殊形式です。aは、「変数aの値」に評価されます。一方で'aはシンボルaそのものに評価されます。(+ 1 2)は3に評価されます。一方で'(+ 1 2)は、シンボル+と1と2のリストである、(+ 1 2)に評価されます。

'aは(quote a)を短く書く記法で、どちらも同じ意味です。

2.4 抽象データの多重表現

システムへの要求が多い場合、複数のデータ表現を1つのシステム内で同時に扱いたいことがあります。

例えば、複素数は直交形式でも極座標形式でも表せます。さらに、どちらの形式が良いかは、それをどのような計算で利用するかによって変わります。したがって、1つのシステムで両方の形式を同時に扱えると便利です。

タイプタグは、データオブジェクトの型（タイプ）を見分けるためのタグです。例えば、直交形式の複素数は'(rectangular (1 2))、極座標形式の複素数は(polar (4 5))のように表せます。

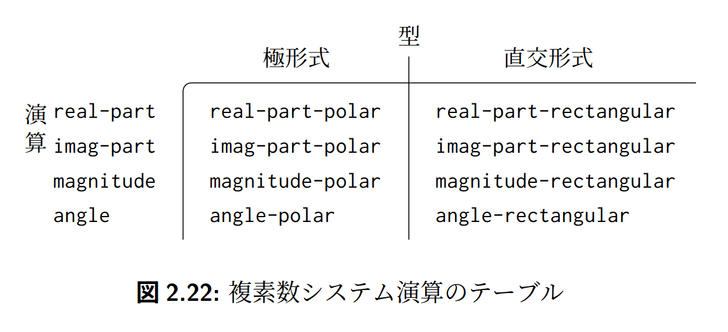
ジェネリック演算とは、複数の型のデータを扱える手続きです。例えば、ジェネリックな実部セレクタreal-partがあるとします。これは直交形式の複素数に適用されると、単にその実部成分を返します。極座標形式の複素数に適用されると、三角関数を駆使して実部を計算して返します。

ジェネリック演算を実装する3つのスタイルがあります。

明示的なディスパッチスタイルは、各ジェネリック演算が、渡されたデータの種類（タイプタグ）によって処理を分岐するスタイルです。プログラムを演算の種類によってグループ化しているといえます。

メッセージパッシングスタイルは、各データオブジェクトが、渡された演算の種類（メッセージ）によって処理を分岐するスタイルです。プログラムをデータの種類によってグループ化しているといえます。これはOOPに繋がります。

データ主導スタイルは、以下のようなテーブルを内部に持つことで、適切な手続きを適用するスタイルです。このスタイルでは、手続きの集合をパッケージと呼びます。パッケージは、自身が公開したい手続きをテーブルに登録します。データ主導スタイルでは、パッケージを演算の種類によっても、データの種類によってもグループ化できます。

新しいデータの種類が頻繁に追加される場合、データの種類によってプログラムをグループ化している方が有利です。演算の種類によってプログラムをグループ化している場合、追加するコードが散らばってしまうことになります。新しい演算の種類が頻繁に追加される場合は逆になります。

3 モジュール性、オブジェクト、状態

3.1 代⼊と局所状態

オブジェクトのふるまいがその過去に影響されるとき、そのオブジェクトは“状態を持つ”と⾔います。

3.1.1 局所状態変数

set!、set-car!、set-cdr!は代入のための特殊形式です。

(set! a 1)は、変数aに1を代入します。

(set-car! pair 1)は、pairのcarに1を代入します。

(set-cdr! pair 1)は、pairのcdrに1を代入します。

3.1.2 代⼊を導⼊する利点

反復版の階乗計算では、状態を表す3つの変数を毎回fact-iterに渡していました。

(define
  (factorial n)
  (fact-iter 1 1 n)
)
(define
  (fact-iter product counter max-count)
  (if (> counter max-count)
    product
    (fact-iter
 	 (* counter product)
 	 (+ counter 1)
 	 max-count
    )
  )
)

代入を用いることで、毎回変数を渡す必要はなくなり、代わりにfact-iterを呼び出す前に変数を変更するだけで良くなります。

3.1.3 代⼊を導⼊することのコスト

代入を導入することのコストは、それによって単純な置換モデルが使用できなくなることです。例えば、導入前は、変数aの値が常に一定であったため、いつでもaを1に置換できました。導入後は、変数aの値が代入の前後で変化するかもしれず、単純に置換できなくなります。

この前後を考えるために、計算モデルに時間の概念が必要になりました。置換モデルには時間の概念はありませんでした。時間は、並行プログラミングを考える上でさらに難しい問題となります。

参照透明性、または参照透過性（referentially transparent）とは、ある式のある部分Aを、Aの値で置換してもプログラム全体の動作が変わらないことです。代入は、参照透過性を破る代表的な機能の1つです。例えば、グローバル変数を参照している手続きがあるとします。代入がない場合は、手続き内の変数を、その値で置換できます。代入がある場合は、変数を参照するタイミングによって、その値が異なります。したがって、単一の値に置換できません。

関数型プログラミング（functional programming）とは、参照透過性を維持するプログラミングスタイルです。本文では、代入を使用しないプログラミングスタイルと説明されます。これは、1章と2章でやってきたようなことです。

命令型プログラミング（imperative programming）とは、参照透過性を維持しないプログラミングスタイルです。本文では、代入を使用するプログラミングスタイルと説明されます。

3.2 評価の環境モデル

代入の導入により、新たに環境モデルを導入します。

環境とは、フレームの順序付き集合です。ある環境Aの次にある環境Bは、Aの外側の環境（enclosing environment）です。

フレームとは、束縛の集合です。

束縛とは、変数と値の対です。

グローバル環境は、一番外側の環境です。基本手続きなどの束縛を持っています。

（ある時点で）ある環境の変数を参照するには、その環境の先頭のフレームから始めて、外に向かって束縛を探索していきます。束縛が見つからない場合、その変数は未束縛（unbound）であるといいます。

3.2.1 評価規則

環境モデルの評価規則は、置換モデルと似ています。

組み合わせを評価するには、

組み合わせ演算子の部分式を評価する。

演算子となっている部分式の値を、被演算子となっている部分式の値に適用する。

ただし、複合手続きのモデルと適用の方法が異なります。

複合手続きは、環境と本体の対です。これはクロージャとも呼ばれます。複合手続きが定義される際、そのときの環境を自身に記録します。

複合手続きの適用は次の手順によって実行されます。

演算子の環境を外側に持つ、新しい環境を作成します。これは環境の継承（extend）とも呼ばれます。
新しい環境の最初のフレームに引数の束縛を作成します。例えば、(square 5)の場合はxと5の束縛を作成します。
新しい環境で演算子の本体を評価します。

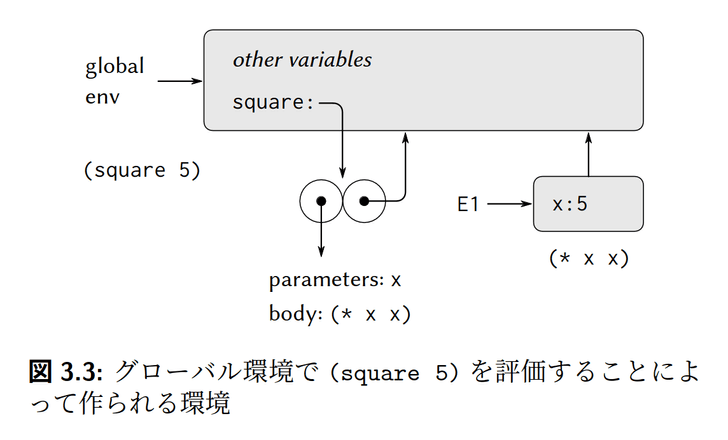
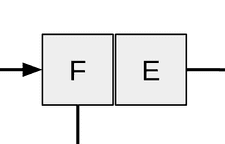
環境を図に描くと以下のようになります。

2つの円がsquareのクロージャです。squareはグローバル環境で定義されたと仮定しています。そのため、クロージャの環境ポインタはグローバルを指しています。E1は(square 5)によって継承された新しい環境です。この環境は、2つのフレームの順序集合です。

3.4 並⾏性: 期限厳守

シリアライザ（serializer）は、手続きをとり、シリアル化された手続きを返す手続きです。同じシリアライザによってシリアライズされた手続きは、それが直列に実行される（並行に実行されることはない）ことが保証されます。シリアライザはミューテックスによって実装できます。

ミューテックス（mutex）は、獲得（acquire）と解放（release）によって操作するデータオブジェクトです。1度ミューテックスが獲得されると、他の獲得は、それが解放されるまで待たされます。

セマフォ（semaphore）は、ミューテックスを同時にn回まで獲得できるようにしたものです。

ミューテックスおよびセマフォは、test-and-set!によって実装できます。

test-and-set!は、変数の参照（test）と代入（set）を一括で直列に（アトミックに）行う基本演算です。これがどのように実現されるかはシステムによります。

アービタ（arbiter）は、test-and-set!のようなアトミックな演算が同時刻に発生した場合に、どの演算を優先させるかを決定するメカニズムです。

最新のマルチプロセスシステムでは、シリアライザは、より新しいバリア同期（barrier synchronization）などの仕組みに取って代わられつつあることにも注意します。

3.5 ストリーム

ストリームとは、遅延リストです。

遅延リストとは、リストの一部が遅延オブジェクトであるリストです。

遅延オブジェクトとは、あるデータオブジェクトの評価を任意の時点まで遅延させることのできるオブジェクトです。遅延オブジェクトは、基本手続きであるdelayとforceによって操作されます。遅延オブジェクトは、Alogolコミュニティではサンク（thunk）とも呼ばれます。式の評価を遅らせることは遅延評価とも呼ばれます。

(delay a)は、aを評価する代わりに遅延オブジェクトを返します。

(force [delayed object])は、遅延オブジェクトの内容を評価して返します。

遅延オブジェクトはメモ化による最適化ができます。最初にforceされた値をオブジェクトがメモしておき、2回目以降のforceではメモの値を返します。この最適化は必要呼びとも呼ばれます。

無限ストリームは、無限の要素を持つストリームです。ただし、実際は遅延オブジェクトによって必要な要素のみが計算されます。

4 メタ⾔語抽象化

メタ⾔語抽象化とは、問題解決のために、それに適した新しい言語を構築することです。

あるプログラミング⾔語の評価器（evaluator）（インタプリタ（interpreter）とも）とは、その⾔語の式に適用されたとき、その式を評価するのに必要なアクションを実⾏するような手続きを指します。

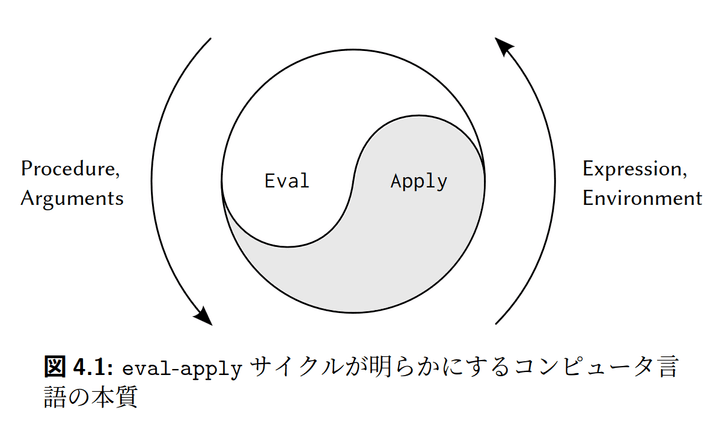
4.1 メタ循環評価器

評価する⾔語と同じ⾔語で書かれた評価器は、メタ循環（metacircular）であると⾔われます。

メタ循環評価器は、本質的には3.2節で記述した評価の環境モデルをSchemeによって形式化したものです。モデルには、以下の二つの基本部品があったことを思い出しましょう。

組み合わせ（特殊形式以外の複合式）を評価するには、部分式をすべて評価し、それから演算子となる部分式の値を被演算子となる部分式の値に適用する。

複合式を引数の集合に適用するには、手続きの本体を新しい環境で評価する。この環境を構築するには、手続きオブジェクトの環境部分にフレームをひとつ加えて拡張し、その中で手続きの仮引数を手続き適用対象の引数に束縛する。

これら二つの規則は、評価プロセスの本質を記述したものです。環境の中で評価する式は引数に適用する手続きに帰着し、それが今度は新しい環境の中で評価する新しい式に帰着し…を繰り返し、環境の中で値が見つかる記号や直接適用する基本手続きにたどり着くまで続けるというのが、評価プロセスの基本サイクルです。

eval は、引数として式と環境を取り、式を分類して評価を振り分けます。

applyは、引数として手続きと、それを適用する引数リストを取り、環境をextendして手続きを適用します。基本手続きと複合手続きの2種類を扱います。

メモ：あまりにも重要なので、ほぼそのまま抜き出しています。

4.2 Schemeの変異版 — 遅延評価

メタ循環評価器を拡張して、正規順序であり、引数の評価が基本手続きで必要になるまで遅延されるSchemeを作成します。

まず、メタ循環評価器に遅延オブジェクト（サンク）を組み込みます。

複合手続きの適用の際に引数を評価するのをやめて、代わりにdelayによって式を遅延オブジェクトで包みます。

基本手続きの適用やifの条件部、REPLの表示部分など、実際の値が必要である場合にforceするようにします。

遅延評価を導入することで、無限ストリームを素直に表現できるようになります。

4.3 Schemeの変異版 — ⾮決定性計算

メタ循環評価器を拡張して、非決定性計算と呼ばれるプログラミングパラダイムを導入します。それは以下のようなものです。

ambは非決定性計算のための特殊形式であり、式を曖昧に返します。

例えば、(amb 1 2 3)を評価し、1が選択されたとします。そのまま計算が進められていき、(amb)を評価するとします。(amb)は、返せる式がないため失敗を意味します。したがって、評価器は(amb 1 2 3)で1を選択したのが間違いだったと判断し、時間を(amb 1 2 3)の時点に巻き戻し、今度は2を選択します。更に失敗すると同様に3が選択され、さらに失敗すると(amb 1 2 3)自体も失敗し、それ以前のambに時間が巻き戻ります。すべてのambが失敗するとそれ以上やることはなくなります。

評価機は、evalとapplyで環境に加えて継続を渡し合います。

継続とは、ある時点での残りの計算（をするために必要なデータ）です。

本実装では、継続は複合手続き（ラムダ式によって作られるクロージャ）です。

evalとapplyは、成功継続と失敗継続を渡し合います。成功継続とは、評価が成功した場合に呼ばれる継続です。失敗継続とは、評価が失敗したときに呼ばれる継続で、その場合変数の代入などが復元され、直前のambの選択に処理が巻き戻ります。

4.4.1 推論的情報検索

メタ循環評価器を拡張して、論理プログラミングパラダイムを導入し、情報検索のためのデータベースインターフェースを実現します。ここで実装する言語は、クエリ言語（query language）と呼ぶことにします。

表明（assertion）は、データベースにおけるデータです。(job (Hacker Alyssa P) (computer programmer))は表明です。

クエリは、ユーザーからのシステムへの問い合わせです。(job ?x ( computer programmer ))はクエリです。?xはパターン変数です。ここでは(job (Hacker Alyssa P) (computer programmer))がヒットします。また、andやor、notを使って複数のクエリをつなげた複合クエリも作成できます。

規則は、クエリの抽象です。以下は規則です。

(rule
  (computer-programmer ?who)
  (job ?who (computer programmer))
)

(computer-programmer ?who)は規則の結論です。(job ?who (computer programmer))は規則の本体です。ここで(computer-programmer ?x)を入力すると(computer-programmer (Hacker Alyssa P))がヒットします。

規則は、Schemeにおける手続きに似ていますが、規則を適用する際の引数に変数が現れうるという特徴があります。

パターンマッチングは、2つのパターンマッチするかを検証し、変数と値の束縛を作成することです。主にクエリと表明に対して使用されます。

例えば、データリスト((a b) c (a b))は、パターン(?x c ?x)にマッチし、このときパターン変数?xは(a b)に束縛されます。

ユニフィケーションまたは単一化とは、2つのパターンがマッチするかを検証し、束縛を作成することです。ここで、クエリと表明のどちらにも変数や値が現れうるのが難しいところです。束縛は変数と値、変数と変数になる場合があります。値と値の束縛は自明なので作成されません。したがって、ユニフィケーションは、パターンマッチングの一般化でもあります。主に規則の適用時に、クエリと規則の結論部分に対して使われます。

この言語の強力な点は、規則に対して多方向の計算ができるというところです。

; 以下の規則を定義する
(rule (append-to-form () ?y ?y))
(rule
  (append-to-form (?u . ?v) ?y (?u . ?z))
  (append-to-form ?v ?y ?z)
)

;;; Query input:
(append-to-form (a b) (c d) ?z)
;;; Query results:
(append-to-form (a b) (c d) (a b c d))

;;; Query input:
(append-to-form (a b) ?y (a b c d))
;;; Query results:
(append-to-form (a b) (c d) (a b c d))

;;; Query input:
(append-to-form ?x ?y (a b c d))
;;; Query results:
(append-to-form () (a b c d) (a b c d))
(append-to-form (a) (b c d) (a b c d))
(append-to-form (a b) (c d) (a b c d))
(append-to-form (a b c) (d) (a b c d))
(append-to-form (a b c d) () (a b c d))

5 レジスタマシンによる計算

Schemeで抽象的なレジスタマシンを定義し、その上にSchemeを実装します。これにより、例えば反復プロセスと再帰プロセスの違いについて明確になります。

レジスタ（register）は、記憶素子です。

スタック（stack）は、後入れ先出しのデータ構造です。任意のレジスタの値をpushしたりpopしたりできます。例えば、マシンがサブルーチンを呼び出すとき、レジスタの内容を後で復元するために使用されます。

マシンは、一連の命令（instruction）を実行します。これはレジスタマシンの機械語にあたります。以下のような命令があります。

goto：特定のラベルにジャンプします。
assign：特定のレジスタへ値をセットします。値はレジスタまたはマシンの基本演算の結果です。
perform：マシンの基本演算を実行します。
test：マシンの基本演算を実行し、その結果が真であったかどうかを記憶します。
branch：直前のtestの結果が真であれば特定のラベルにジャンプします。
save：特定のレジスタをスタックにpushします。
restore：スタックから値をpopし、特定のレジスタにセットします。

マシンはGC（ガベージコレクション）を持つものとします。GCは不要になった（レジスタやスタックから到達できない）データオブジェクトを破棄する仕組みです。GCを実現するいくつかのアルゴリズムがあります。ストップ＆コピーは、本文で紹介されているアルゴリズムで、実行後に必要なデータオブジェクトの位置を圧縮（compacting）できるという利点があります。

明示的制御評価器（explicit-control evaluator）は、Schemeのメタ循環評価器をレジスタマシンに実装したものです。簡単のために、ここではevalとapplyのみを実装し、それ以外はマシンの基本演算とします。

明示的制御評価器では、ある手続きの最後（末尾）の処理が手続きの適用である場合、スタックに何も保存せず適用を処理できることを示します。これは、反復プロセスがメモリを消費せずに自身を再帰的に呼び出せる理由です。

コンパイラ（compiler）は、ソース言語で書かれたプログラムを、そのマシンのネイティブ言語（機械語）で書かれたプログラムに変換します。ここでは、Schemeで書かれたプログラムを、レジスタマシンの命令列に変換します。コンパイラの構造はインタプリタに似ていますが、式をその場で評価するのではなく、評価のための等価な命令列を生成し、それらを集積するというところが違います。

インタプリタはマシンをユーザープログラムのレベルに上げるもので、コンパイラはユーザープログラムを機械語のレベルに落とすものです。

つまり、この章で実装したSchemeインタプリタがなければ、私達はレジスタマシンの機械語（命令列）でプログラミングすることになります。インタプリタのおかげで、マシンがユーザープログラムのレベルに引き上げられ、Schemeでプログラミングできるようになります。対象的に、コンパイラは私達が書くSchemeのプログラムをレジスタマシンの機械語に変換します。

Scheme⾔語は（Scheme⾔語だけでなく、どんなプログラミング⾔語でも）、機械語の上に建てられた⼀貫性のある抽象化の⼀族と見なすことができます。

インタプリタは、プログラム実⾏のステップがこれらの抽象化によって構成されていて、そのことによってプログラマに理解しやすくなっているため、対話的プログラム開発やデバッグに向いています。コンパイル済みコードは、プログラム実⾏のステップが機械語によって構成されており、またコンパイラは⾼レベルの抽象化の壁を越えて最適化を⾃由に⾏えるため、実⾏速度が速くなります。

まとめ

'doneです。おつかれさまでした。もしこのノートが何かの役に立つのならうれしいです。

ありがとうございました。