SICPの感想文

2023/07/29

今年のお正月に、「無料で読めるポール・グレアムの「ハッカーと画家」+αの日本語訳のみのまとめ」がエントリに上がっていて、布団にこもりながらダラダラ眺めていたところ、前からSICPが気になっていたのを思い出した¹ので、「いい機会だし読んでみるか〜」となり、約7ヶ月かかって読み終わりました。

計算機プログラムの構造と解釈（Structure and Interpretation of Computer Programs）は、計算機科学の古典であり、MITのプログラミング入門講義で教科書として使用されていた本です。

通称、タイトルの頭文字をとってSICP（しくぴー）とか、表紙の絵から魔術師本とか、表紙の色から紫本などと呼ばれます。原文および日本語訳は無料で公開されています。日本語訳にもいくつかあるのですが、私は真鍋氏のものを読ませていただきました。

取り組むにあたって、すべての練習問題に回答することにしました。わからない問題は、1日以上考えてもダメならネットで先人の回答を検索しても良いことにしました。ただし、練習問題4.79に含まれる「博士号が取れる自由回答問題」だけはスキップしています。（後述します）

最終的な私の回答は以下にあります。他の人の回答や資料を参考にした場合は、参考元をコメント等で記載してあります。可能な限り裏取りをしていますが、間違いがあるかもしれません。しかし、私は先人の回答に助けられた場面が多かったので、これもなにかの役に立てばと思います。

https://github.com/sititou70/sicp-exercises

この記事はSICPの読書感想文です。あまり難しい説明をせず、SICPを読んで感じたことを書きます。備忘録は別で書きました。

献辞、前書き、序文、謝辞

この本を、尊敬と賛美を込めて、コンピュータの中に住む妖精に捧げます。

出典：SICP 非公式日本語版翻訳改訂版、以降同じものについて出典略

だったり、

プログラムは⼈間が読めるように書かなくてはならず、それがたまたま機械によって実行できるというだけのことです。

だったり、いろいろと有名なやつが並びます。事前に読んでおくとモチベーションが高まります。SICPを終えたあとにもう一度読み直すと、「あ〜わかる」という気持ちになります。

1章

この本ではLispの方言であるSchemeを使います。1章では、Schemeの基本的な文法等について主に学びました。ここは特に苦労しませんでした。

だったら退屈だったのか？

というと、決してそんなことはありません。

Schemeの導入以外にも、以下のような「どこかで聞いた気がするけど自信を持って説明できない」トピックがあり、勉強になりました。

宣言的知識と手続き的知識
適用順序と正規順序
反復プロセスと再帰プロセス
- 再帰手続きと再帰プロセスの違い
- 末尾再帰
増加オーダー

特に、増加オーダーの件で $Θ$ （シータ）記法というものがあるのを初めて知りました。世間的によく使われるのは $O$ （ビッグオー）記法だと思います。私が今まで $O$ 記法として使っていたのは、ほとんど $Θ$ 記法の意味であり、盛大に勘違いしていました。

簡単に言うと、「計算量は $Θ(n)$ だ」または「 $O(n)$ だ」というとき、 $Θ$ 記法は計算量を $n$ の定数倍で上下からはさみます。 $O$ 記法は $n$ の定数倍で上からしか抑えません。

1章の練習問題

練習問題は思ったよりも多かったです。例えば、以下のような題材を扱います。

逐次近似、ニュートン法、不動点、黄金比の近似、根の近似
アッカーマン関数、テトレーション
フィボナッチ数、一般項、対数時間でフィボナッチ数を求める方法（行列の結合性を使う方法は知っていたのですが、SICPの方法はそれよりも早く、感動しました）
パスカルの三角形
両替問題（特定の金額を表すための硬貨の枚数の組み合わせ）
ユークリッドの互除法
素数判定、素朴な方法、確率的判定、合同式、フェルマーテスト、カーマイケル数、ミラーラビンテスト
数値積分、シンプソンの公式
無限連分数、自然対数の底の近似、tanの近似

「あー、入門としては定番だよね」というものから、「そこまでやる……？」というものまであります。特に素数判定のあたり。

高校で合同式を習っていなかったので、「合同式(mod)の意味とよく使う６つの性質 | 高校数学の美しい物語」とか、「【高校数学(発展)】合同式①(modとは何か)【整数】」とかを見てました。最近はこういうわかりやすいやつがあるので最高ですね。

そのうえで「結局わからん」となりながらフェルマーテストの原理を追ってました。

「この前の休日？あぁ、フェルマーの小定理について考えてたよ」

って、なんかかっこよくないですか。

このへんで「そういえば練習問題って全部で何問くらいあるんだろう」と思い、集計したのが以下の表です。

章	問題の数
1	46問
2	97問
3	82問
4	79問
5	52問

泣いちゃった

2章

プログラムを読みやすくするために、 Lispはcarとcdrの代わりにfirstとrestを使うべきだとしばしば言われて来た。ま、最初の2時間くらいはそうかもしれない。だがハッカーは、carはリストの最初の要素でcdrは残りの要素だなんてことくらいすぐに覚えられる。

出典：人気の言語を作るには ---Being Popular---

とのことで、私がハッカーかはわかりませんが、確かに数時間で慣れました。

map、filter、accumulate

map、filter、accumulateが出てきました。私はお仕事でJavaScriptを扱うので、これがArray.prototypeのmap、filter、reduceに対応することがすぐにわかりました。

ただ、Schemeのmapとaccumulate（foldとも）は、JSのものよりも一般化されているのが面白かったです。

JSのmapは、「1つのリスト（配列）」と「1引数の関数」で動作します。リストのi番目の要素を関数の引数に渡して、その戻り値であたらしいリストが作られます。

Schemeの一般化されたmapは、「n個のリスト」と「n引数の関数」で動作します。n個のリストのi番目の要素を関数の引数に渡して、その戻り値であたらしいリストが作られます。

これがJSのmapの自然な拡張になっているのが美しいなと思いました。accumulateも同様で、複数のリストを自然な形で渡せます。

データ

「データとは何か」という節が興味深かったです。ここでは、データとは「コンストラクタ、セレクタ、満たさなければならない条件」の3つによって定義されるものと説明されます。

例えば「分数」データがあるとします。分数のコンストラクタとセレクタは以下のように実装できます。

// 分数コンストラクタ
function makeFraction(numer, denom) {
  return [numer, denom];
}
// 分数セレクタ
function getNumer(fraction) {
  return fraction[0];
}
function getDenom(fraction) {
  return fraction[1];
}

満たさなければならない条件とは以下です。

getNumer(makeFraction(a, b)) === a
getDenom(makeFraction(a, b)) === b

これらの3つが何らかの方法で実現されているなら、その実装言語、内部表現、デジタルかアナログかなどに関係なく、それは分数データに見えるし、そのように振る舞うだろうということみたいです。

なるほどね？

メッセージパッシングと型によるディスパッチ

データ抽象化の文脈でメッセージパッシングが登場しました。

面白かったのは、メッセージパッシングスタイルは、プログラムをデータの種類（型）によってグループ化しているという視点でした。

それとは逆に、演算の種類によってプログラムをグループ化すると、型によるディスパッチスタイルにつながるというのも興味深いです。

いままではこれら2つをそのように結びつけて考えていなかったので新鮮でした。

2章の練習問題

練習問題は案の定多くて大変でした。好きなやつを2つ紹介します。

1つは、以下のような1950年代のロックの歌詞をハフマン符号木によって圧縮する問題です。

Get a job
Sha na na na na na na na na
Get a job
Sha na na na na na na na na
Wah yip yip yip yip yip yip yip yip yip
Sha boom

なるほど。圧縮に対する やりがい を感じます。

もう1つは、文字式の演算をする問題です。例えば以下のようなプログラムを書きます。

(define p1 (make-polynomial 'x '((1 1) (0 1))))
(define p2 (make-polynomial 'x '((3 1) (0 -1))))
(define p3 (make-polynomial 'x '((1 1))))
(define p4 (make-polynomial 'x '((2 1) (0 -1))))
(define rf1 (make-rational p1 p2))
(define rf2 (make-rational p3 p4))
(add rf1 rf2)

数式で書くと以下のようになります。

\frac{x + 1}{x^3 - 1} + \frac{x}{x^2 - 1}

ようするに分数の足し算です。

実行すると以下が出力されます。

'(rational
  (polynomial x (3 -1) (2 -2) (1 -3) (0 -1))
   polynomial x (4 -1) (3 -1) (1 1) (0 1))

数式で書くと、

\frac{- x^3 - 2x^2 - 3x - 1}{- x^4 - x^3 + x + 1}

正しく計算できているのがわかります。

まぁたったこれだけなんですが、内部では

多項式の除算
多項式の最大公約数（？）
- ユークリッドの互除法の拡張
- ユークリッド環（？）
- 測度（？）
整数化因子（？）
擬除算（？）と擬剰余（？）

といった手法ないし概念が使われています。正直原理はよくわかっていません。特に、分数を既約にするためにこれらが必要です。

ちなみに、今回は登場する文字が $x$ だけだったのでまだ良かったのですが、ここに他の文字が追加されると、「型階層を見直して強制型変換で……」のようにさらにヤバくなります。

ちょっと油断していると、SICPがプログラミング入門の教科書であったことを忘れてしまいます。

まぁここで難しいのはプログラミングというよりは数学ですが、いずれにせよ MITってやべーな という気持ちと、じゃあテイラー展開とかフーリエ変換とかできる本格的な数式処理システムってどうなってんの……？ という気持ちです。

3章

代入

「代入」という概念が登場しました。そういえばこれまで代入を使ってこなかったな〜〜という感覚です

ここで、

関数型プログラミングとは、代入を使用しないプログラミングスタイルである
命令型プログラミングとは、代入を使用するプログラミングスタイルである

と説明されていて、「そうだったのか」という気持ちになりました。

また本文では、より厳密に参照透過性を引き合いに出しても説明しています。代入は、参照透過性を破ってしまう代表的な機能の1つです。

これまでは 関数型プログラミングって何？ と聞かれたら

えっと……関数を組み合わせてプログラミングすることだよ。

……それは関数型プログラミング以外でもそうじゃない？

いやでも、mapとかfilterとか便利なやつがあって、あとモナドっていうのがあるらしくて……

ふーん？

という、ふんわりした説明しかできなかったと思います。

もちろんすべての言語に当てはまる定義ではないとは思いますが、理解度が高まって良かったです。

環境モデル

代入によって、それを格納する「環境」が必要になるということで、環境モデルを学びました。

環境とは、フレームの順序付き集合である。
- ここで、ある環境Aの次にある環境Bは、Aの外側の環境（enclosing environment）である。
フレームとは、束縛の集合である。
束縛とは、変数と値の対である。

と理解しました。

また、クロージャとは、「手続き（関数の本体）」と「それが評価（作成）された環境」の対であるとも理解しました。クロージャはその評価時に、その時点の環境を自身に保存します。そして適用時に、その環境をextendsした環境を作成し、そこで自身の手続きを評価します。

レキシカル環境とかクロージャとか束縛とか、JavaScriptの文脈でも聞く用語が並んでいて面白かったです。「JavaScriptはSchemeの影響を受けている」という話を聞いたことがあって、この辺がそうなのかもな〜と思いました。

まぁ、これはSchemeの説明なので、JSの実際の事情はECMA-262を参照すべきです。

がっつり読めてはいないのですが、例えば10.2 ECMAScript Function Objectsを参照すると、関数オブジェクトの内部スロットに [[ECMAScriptCode]] と [[Environment]] があり、「手続き」と「環境」の対に相当するものがあるとわかります。

関数評価（作成）時の抽象操作であるOrdinaryFunctionCreateを見ると、 13. Set F.[[Environment]] to env. というステップがあり、その時点の環境を自身に保存しているのがわかります。また、関数呼び出しの抽象操作である[[Call]]から呼ばれるPrepareForOrdinaryCallから呼ばれるNewFunctionEnvironmentでは、 6. Set env.[[OuterEnv]] to F.[[Environment]]. というステップがあり、先程保存した環境を外部環境として新しい環境を作成（extends）しているとわかります。

ストリーム

SICPでは、「要素の一部が遅延オブジェクトであるリスト」をストリームと呼んでいます。

遅延オブジェクトのおかげで、必要な要素のみが計算され、無限の要素を持つストリームを表現できるということを学びました。

せっかくなのでストリームをJSで実装してみました。パズル的な面白さがあるので、暇な方だけ見ていただければと思います。

// 遅延オブジェクトは関数で表現することにする

// 遅延オブジェクトの作成するには次のように書く：() => 評価を遅延したい式

// 遅延オブジェクトを評価する。遅延オブジェクトでなければ何もしない
const force = (value) => (typeof value === "function" ? value() : value);

// streamを構築する。次のように残りのstreamを遅延させて呼び出す：consStream(streamの最初の要素, () => 残りのstream)
const consStream = (first, rest) => [first, rest];
// streamの先頭の要素を得る
const streamCar = (s) => s[0];
// 残りのstreamを得る
const streamCdr = (s) => force(s[1]);

// mapのstream版
const streamMap = (proc, ...streams) =>
  consStream(
    //
    proc(...streams.map(streamCar)),
    () => streamMap(proc, ...streams.map(streamCdr))
  );

// 2つのstreamの各要素を足したstreamを得る
const addStreams = (s1, s2) => streamMap((v1, v2) => v1 + v2, s1, s2);

// streamを先頭からn個表示する
const printStream = (stream, n) => {
  let s = stream;
  for (let i = 0; i < n; i++) {
    console.log(streamCar(s));
    s = streamCdr(s);
  }
};

// main
const ones = consStream(1, () => ones);
printStream(ones, 5);
// 1
// 1
// 1
// 1
// 1

const integers = consStream(1, () => addStreams(ones, integers));
printStream(integers, 5);
// 1
// 2
// 3
// 4
// 5

const fibs = consStream(
  0,
  consStream(1, () => addStreams(streamCdr(fibs), fibs))
);
printStream(fibs, 10);
// 0
// 1
// 1
// 2
// 3
// 5
// 8
// 13
// 21
// 34

ones、integers、fibsが、なぜ所望のストリームを表示するか、ぱっと見てわかりますか？

サクッとわかったあなたは人間ではありません。私のような普通の人間は、この節で頭が爆発します。

SICPには更に複雑なものが載っています。素数のストリームを作ってみたり、tanのべき級数を求めてみたり、円周率をエイトケン加速で近似してみたり、電子回路をシミュレートしてみたり、微分方程式を解いてみたりと、やりたい放題です。こわいです。

4章

4章がSICPのメインディッシュです。

メタ循環評価器

メタ循環評価器とは、あるプログラミング言語上で構築された、そのプログラミング言語のインタプリタです。つまり、この節ではSchemeでScheme（のインタプリタ）を作ります。

そんなことして何になるんだ？

と思われるかもしれません。私は思いました。

この節より後では、解きたい問題に対して、それに適した新たな言語を作ります（！）

メタ循環評価器は、そのためのベースラインとなります。

評価器の仕組み

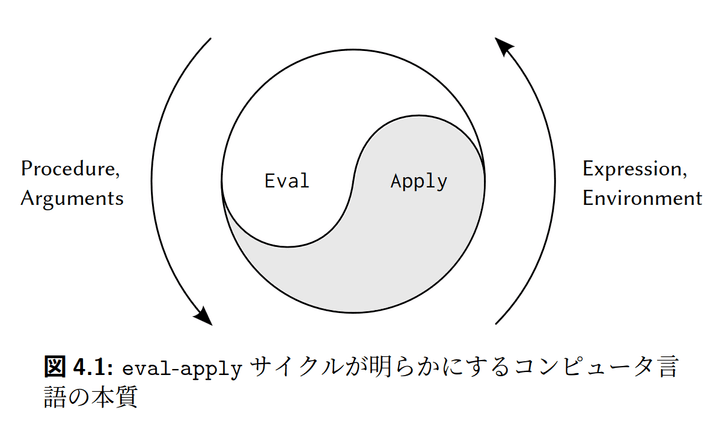
評価器は、evalとapplyの相互再帰呼出しによって動作していきます。

evalは環境で式を評価します。式が手続き適用であればapplyを呼び出します。applyは適用を処理します。手続きが複合手続きであれば環境をextendし、その中で本体を評価するためにevalを呼び出します。

このようにeval、apply、eval、apply……と互いに呼び出し合う様子を表したのが以下の図で、おそらくSICPで最も重要かつ有名な図です。

あまりに重要なので、よく見ると表紙にも描かれています。

遅延評価

なんと、メタ循環評価器を少し改造するだけで、遅延評価版のSchemeが作れてしまうので感動します。

基層のSchemeは適用順序なのに、そのうえで正規順序Schemeが動作するのは、インタプリタが基層言語の1つ上の抽象レベルに引き上げてくれるからです。

遅延評価で嬉しいことはいくつかあるのですが、例えば無限ストリームが素直に書けるようになります。前述したJSのストリームは、遅延オブジェクトを明示的に扱っていました。

const ones = consStream(1, () => ones);

これは、本当は次のように書きたいのですが、

const ones = consStream(1, ones);
// ReferenceError: Cannot access 'ones' before initialization

適用順序評価の環境だと、onesを初期化する前に参照してしまいうまく行きません。

ところが正規順序評価の環境では、引数の評価は必要になるまで評価が遅延されるため、このようにきれいに書けるのです。やった〜〜

⾮決定性計算

非決定性計算は、まるで時間が巻き戻るようなプログラミングパラダイムです。SFみを感じます。

ambは、いくつかの式に「曖昧に」評価される特別な式です。JSで無理やり表現すると、次のようになります。

const a = amb(1, 2);
const b = amb(3, 4);
console.log([a, b]);

このプログラムを実行すると、[1, 3]と表示され、いったん停止します。しかし、非決定性計算の環境では、「他の可能性は？」と処理系に尋ねることができます。

そうすると、処理系は最後のambの時点に 時間を戻して 、bへの代入を別の選択肢である4でやり直し、[1, 4]を表示します。

さらに「他の可能性は？」と尋ねると、amb(3, 4)で取れる選択肢はなくなったため、それより前のamb(1, 2)に戻ってaの代入を2でやり直し、[2, 3]が表示されます。更に尋ねると、同様に[2, 4]が表示され、更に尋ねると「これ以上の可能性はない」と返します。

まるでambのたびに世界線が分岐しているようにも見えます。SICPには、このパラダイムを使って様々な論理パズルを解く方法が載っており、とても面白いため興味のある方は参照されると良いと思います。

これを実現するために、evalとapplyは、成功継続（ambが成功した場合の残りの計算）と失敗継続（ambが失敗した、つまり選択肢がない場合に実行すべき残りの計算、前のambの残りの選択肢を選ぶ処理だったり、代入を復元する処理だったり）を渡し合います。

ここらへんで「継続」という用語があまり怖くなくなった気がします。

論理プログラミング

「論理プログラミング」というと馴染みが薄く戸惑ってしまうのですが、「Prolog」と言われると「なんか聞いたことあるわね」となりました。いや聞いたことがあるだけで、触ったことはないんですけども。

この節で私が一番驚いたのは、手続きが双方向に計算できるということです。

例によってJSで説明します。

例えば、以下のようなappend関数を実装²し、実行したとします。

const append = (list1, list2) => [...list1, ...list2];
console.log(append([1, 2], [3, 4]));
// [1, 2, 3, 4]

これは「append([1, 2], [3, 4])の結果は？」という質問に処理系が答えてくれたということになります。ここまでが普通のプログラミングです。

しかし論理プログラミングの処理系では、「結果が[1, 2, 3, 4]となるappend([1, 2], ?x)は？」と質問することもできます。?xはパターン変数と呼ばれる特殊な記法で、命名は適当です。

これには「append([1, 2], [3, 4])」という回答が返ります。

さらに、「結果が[1, 2, 3, 4]となるappend(?x, ?y)は？」と質問することもできます。この場合、

append([], [1, 2, 3, 4]);
append([1], [2, 3, 4]);
append([1, 2], [3, 4]);
append([1, 2, 3], [4]);
append([1, 2, 3, 4], []);

が回答されます。

まるで出力から入力を、結論から仮定を推論しているようで、「なんでこんなことができるんだ……？」と感心してしまいます。

このような挙動を実現するために、ユニフィケーション（単一化）というアルゴリズムを学びました。これは進化版applyといった感じです。

これまでの関数適用は、変数と値の対を扱えばいいので簡単でした。例えば、append([1, 2], [3, 4])を適用するときは、「list1と[1, 2]の束縛」、「list2と[3, 4]の束縛」を作れば良いです。

一方で、append(?x, ?y)を処理する場合、実引数側にも変数が現れます。またここでは説明しませんでしたが、仮引数側に値が現れることもあります。しかもその値は複雑な複合オブジェクトであるかもしれず、さらに中に変数を含んでいるかもしれません。また、実引数側の変数名と仮引数側の変数名が衝突する場合も考えられます。これを考慮しないと、最終的な推論がうまく行きません。

などなど、いろいろ難しい論理プログラミングですが、そのパワーはすごいものだと感じました。Prologは全くわからないのですが、そのメカニズムの重要な部分に単一化が関わっていそうだという感覚を持てました。

自由回答問題

4章には唯一スキップした練習問題があります。以下は練習問題4.79です、

練習問題 4.79: 4.1節でLisp評価器を実装したとき、局所環境を使って別々の手続きの引数同士で名前が衝突しないようにする方法を学んだ。

（略）

クエリ⾔語で、変数のリネームではなく、環境を使う規則適⽤の手法を実装せよ。その環境構造の上に、ブロック構造手続きの規則版のような、大規模システムを扱うためのクエリ⾔語の構築物を作ることはできるだろうか。これらの問題と、問題解決の手法として文脈の中で推論を行うという問題（例えば、"もしPが真であると仮定すると、AとBが推論できる"）とを関連づけることはできるか。（この問題は自由回答だ。うまい解答ができれば博士号が取れるだろう。）

スキップしたのは「これらの問題と、問題解決の手法として文脈の中で推論を行うという問題（例えば、"もしPが真であると仮定すると、AとBが推論できる"）とを関連づけることはできるか。」の部分で、自由回答とされています。

正直、何を問われているのかもわかりません。手も足もでません。おそらく、先程書いた「結論から仮定を推論しているよう」が関連している気はするのですが、「博士号をとりたくなったらまた考えることにする」というふざけたコメントでお茶をまぜまぜしておきました。

5章

仮想的なレジスタマシンのエミュレータを実装し、その機械語のうえで4章のメタ循環評価器を実装しました。

これにより、例えばSchemeはどのようにしてメモリを消費せずに末尾呼び出しを行っているかという疑問が解決します。

実際に、手続きの最後の処理が手続き呼び出しである場合、その後呼び出しの後何もすることがない（継続がない）ため、スタックに何も積まず次の手続きへgotoできることが示されます。なんでも継続で、「継続の考え方を使うと末尾再帰の最適化は自然に導かれる」と言っていた意味がちょっとわかった気がします。

また、Schemeのプログラムを仮想マシンの命令列に変換するコンパイラも実装しました。ここらへんまで来ると、自分が何をやっているのかよくわからなくなってきます。

5章の練習問題

最後の2問の練習問題、5.51と5.52がSICPのラスボスです。

5.51

練習問題 5.51: 5.4節の明示制御評価器を翻訳することによって、C言語（または好きな低レベル言語）によるSchemeの基本的な実装を開発せよ。このコードを動かすためには、適切なメモリ割り当てルーチンや、その他の実行時サポートを用意する必要があるだろう。

一見するとけっこうヤバいことを言っているようですが、実際ヤバいです。

次のようになりました。

データオブジェクトの表現
- Schemeの数値：すべて浮動小数点数にする
- Schemeの文字列：サポートしない
- Schemeのシンボル：文字列
- Schemeのペア：ポインタ2つの構造体
GC：単純なmark-and-sweep
パーサ：再帰下降構文解析を勘で実装

デモのために、以下のようなSchemeの各言語機能を試す簡単なプログラムsample.rktを作成しました。

#lang racket

; self-evaluating
(displayln 1)
; 1

; quote
(displayln 'quote_value)
(displayln '2)
; (quote quote_value)
; 2

; definition, variable assignment
(define a 3)
(displayln a)
(set! a 4)
(displayln a)
; 3
; 4
; ...

sample.rktのすべてのコード

sample.rktは、もちろんSchemeの処理系（今回はRacketを使用）で実行できます。

$ racket sample.rkt
1
quote_value
2
3
4
# ...

そして、今回作成したインタプリタでも実行できます。

$ make && ./main sample.rkt
make: 'default' に対して行うべき事はありません.
1.000000
quote_value
2.000000
3.000000
4.000000
# ...

今回、CUnitによるC言語のテストを初めて書いてみたのですが、めちゃくちゃ快適でした。70件のテストに2.7秒しかかかりません。

このうち3件は、1万回データオブジェクトを生成してGCを試したり、10万回の末尾呼び出しで末尾再帰をテストしたり、まったくの最適化なしで25番目のフィボナッチ数をevalするといった極端なものです。

それらを除外すると、テストは0.15秒で終わります。今回の実装では、いじっているところと全く関係ない部分のテストが落ちたりしてたので、テスト全体を素早く実行できるのは大変助かりました。

実装上妥協した点がいくつかあります。例えば、型情報の保持にTagged pointerを使ってみたかったのですが諦めました。私自身、CPUやメモリに詳しくないということと、変なハマり方を避けて、いったん動くところを目指したかったからです。他にも、null値が同値でなかったり、同じ文字列のシンボルなのに個別でmallocしていたりと、わかる人からすると効率の悪いところが結構あります。ゆるして……

だいたい10日くらいでsample.rktが動くようになりました。

5.52

練習問題 5.52: 練習問題 5.51と対応するものとして、コンパイラを修正してSchemeの手続きをC言語の命令列にコンパイルするようにせよ。4.1節のメタ循環評価器をコンパイルして、C言語で書かれたSchemeインタプリタを生成せよ。

実は5.51の一部を流用できるため、追加の実装はそこまで多くありません。

いじるのはSchemeなので、デバッグもしやすいですしね。

……と思っていたのですが、ここにきて5.51側のバグがやっぱり見つかったので、けっきょくC言語の世界にreturnしました。

そのバグというのがどれも結構厄介で、ちょっと考えたくらいではわからないものでした。ここでは、地道に原因を追求していくのが近道なんだなぁということを改めて学びました。

例えば、上層のSchemeで「変数を定義した後、その直後は変数を参照できるが、数行以上経過するとUnboundになる」というバグがありました。普通にプログラミングしている分にはまずありえない状況なので、一周回ってウケちゃいますね。

ぼく「まずは、これがコンパイラのバグなのか、レジスタマシンのバグなのかを切り分けよう……。生成されたCのコードを読んでみると、コンパイラは問題なさそうだ。じゃあレジスタマシンの基本演算の実装がおかしい？いや、SICPのをほぼそのまま移植しているので大丈夫なはず……。よくわからんから環境をユーティリティでprintデバッグしてみよう。あれ、環境をprintするとセグフォするぞ……。しかもprintしてもセグフォしない環境もある……？これはまずユーティリティのバグを直さないと……」

といった感じです。結論としては、GCが微妙なタイミングで起きるとダメとか、mallocの数を±1だけ間違ってたとか、そういう細かい原因でした。

そんなこんなを繰り返して3日経ったころ、ようやくサンプルコードやメタ循環評価器が動くようになりました。

まず、sample.rktをコンパイルしてみます。

$ racket compile-to-c.rkt sample.rkt > main.c && wc main.c
1631  2607 45829 main.c

コンパイルの結果、1,631行のCのコードが生成されました。これを更にコンパイルして実行してみると……

$ ./main
1.000000
quote_value
2.000000
3.000000
4.000000
# ...

確かにsample.rktが実行されました。

次に、m-eval.rktをコンパイルしてみます。これは4章のメタ循環評価器です。

$ racket compile-to-c.rkt m-eval.rkt > main.c && wc main.c
8334  13665 247755 main.c

コンパイルの結果、8,334行のCのコードが生成されました。うおお

これを更にコンパイルして、sample.rktを指定して実行してみると……

$ ./main sample.rkt
1.000000
quote_value
2.000000
3.000000
4.000000
# ...

sample.rktが実行されました！

ちなみに、これまでの環境でsample.rktの実行時間を比較してみます。20回の計測の平均をとりました。

環境	sample.rktの実行時間
Racket	408.1 ms
Cで実装したインタプリタ	11.6 ms
Cへのコンパイル	8.8 ms
メタ循環評価器をコンパイルして作成したインタプリタ	614.6 ms

RacketがCのインタプリタやコンパイルよりも遅いのは、標準ライブラリを読み込んでたり、いろいろ実用的な機能を備えているからだと思います。

インタプリタに比べて、コンパイルすると若干早くなってますね。

メタ循環評価器をコンパイルした環境はさすがに遅いです。他の環境と違って、マシン組み込みとしていた演算の一部を自分で処理しているので、メモリ使用量が多く、GCも複数回発生していました。

解釈とコンパイル

ここまでやることで、以下の説明にだいぶ納得感が出ました。

インタプリタはマシンをユーザープログラムのレベルに上げるもので、コンパイラはユーザープログラムを機械語のレベルに落とすものです。

4章では、遅延評価、非決定性計算、論理プログラミングなどのいろいろなインタプリタを書いてSchemeのレベルを上げました。

5章では、コンパイラによってSchemeをレジスタマシンの命令列やC言語に変換し、レベルを落としました。

今まで、インタプリタとコンパイラはそれぞれ全くの別物というイメージでした。しかし、（少なくともSICPにおいては）その原理的な部分は結構似ているし、レベルを上げるものと落とすものという、対称性があることもわかりました。

まとめ

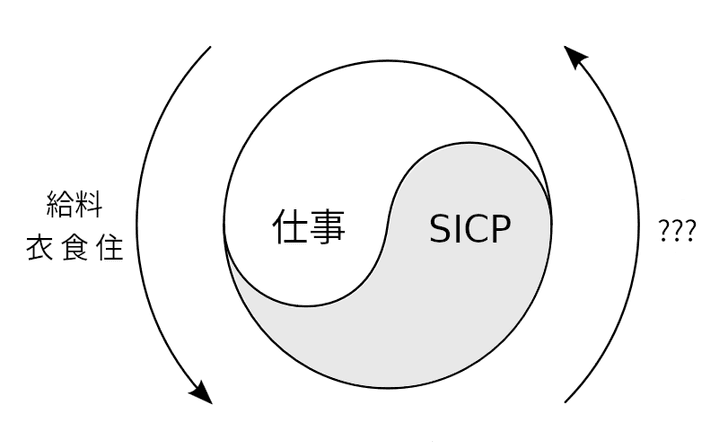
お正月からSICPを読み始め、仕事、SICP、仕事、SICP……のサイクルを回してきました。

仕事はSICPを読むための衣食住を提供します。ではSICPが仕事にどう役立つのかというと、読んだ直後なのでまだよくわかっていません。

ただ、SICPによって、今までぼやけていた部分が鮮明になった気がします。プロセスとはなにか、データとはなにかなど、そういう基礎的な部分は、仕事に限らず、今後いろいろなことを考える際に効いてくる気がしています。

練習問題を（自由回答を除いて）すべて解いたのは良かったです。私は他人と比べて理解力が弱いので、問題を解くことではじめて自分の勘違いに気づけましたし、他の人の回答と比べることで理解が深まりました。

SICPのすべてを理解したとは思っていないので、間違いがありましたらご指摘いただけると嬉しいです。

著者、翻訳者、TeX、LaTeX周りを整備してくださった方、先人の回答、その他すべての関係者に感謝します。

ここまで読んでいただきありがとうございました。

「前」とは小学生のころで、当時、パソコンもインターネット環境も無いが漠然とハッカーに憧れていた田舎のクソガキの私は、ジャスコ（死語）に入っていた本屋の書籍検索に「ハッカー」と打ち込み、唯一ヒットした「ハッカーと画家」を立ち読みしていました。そこでポール・グレアム氏が「プログラミングに関して皆に一つだけ引用文句を覚えてもらえるならば」としてSICPの冒頭を挙げているのを見て、「すごいハッカーが引用するくらいだから元の本もすごいんだろう」と漠然と感じた記憶を思い出しました。↩
本文における実際のappendの実装は、これとは異なりもう少し複雑です。ここではあくまでも例であることをご了承ください↩