TypeScriptの型で全加算器から浮動小数点数,そして√2
2021/06/07またも懲りずにTSの型パズルで遊んだ結果, が計算できましたので報告します.よろしくおねがいします 🙇
リポジトリ:ts-sqrt-type
TypeScriptと型パズル
TypeScriptまたはTSとはプログラミング言語の一種であり,JavaScript feat. 型システム という感じで,式で表すと,
となります.JavaScriptなどの一般的なプログラミング言語がチューリング完全なのは当然ですが,TSの型システムもチューリング完全というのはあまり知られていないかもしれません.つまり,
となりますから,TSは他の言語より2倍もチューリング完全なのでお得なんですね.は?
話が墜落しましたが,ここで言いたいのは「今回はJavaScriptを一切書かずに,TSの型システムだけでプログラミング(型パズル)するよ」ということです.
Step 1:自然数の表現を定義する
型の世界には四則演算はもちろん,自然数すらありません.
「型で自然数をどう表現しますか?」
と聞かれて真っ先に思いつくのは1型や2型といったnumberのリテラル型を用いる方法ですが,これはあまり役に立ちません.number型のままでは「ある数の次の数」すら求められませんし,まして四則演算なんて無理すぎます.
では他の型パズラーの皆様はというと,関数型がお好きな方々は,
チャーチ数だ! !
といって簡約を繰り返したり,また基礎論がお好きな方々は,
ZFCを認めて,!
といって集合の集合を持ち出したりと,個性的な人たちですね.
私はソフトウェアエンジニアでありコンピュータが好きなので,今回は次のような2進整数を使うことにしました.
type Bit = 0 | 1;
type Bits = Bit[];
// example
const four: Bits = [0, 0, 1];
// LSB <---> MSB配列の0番地に最下位ビットが入ります.コードで書くときは普段の表記(下位の桁を右に書くやつ)と逆になるので注意です.
Step 2:自然数の四則演算を実装する
足し算
複数桁の2進数を扱う前に,まずは1ビットの足し算を実装します.そう…
全加算器…基本情報の試験勉強で一瞬聞いた気がするくらいの認識ですが,実はすべての計算の根本を担う偉いやつです.全加算器は,筆算の1桁分を計算することに対応します.みなさんが足し算の筆算の1桁分を考えるときは,
- 前の位からの桁上がり(carry in)
- 足される数の現在の位
- 足す数の現在の位
…の3つを考慮して,
- 現在の位の答え
- 次の位への桁上がり(carry out)
…の2つを出力すると思います.全加算器も3入力2出力の回路で,2進数においてすべてのパターンを書き下すとFullAdder型は以下のように実装できます.
type AdderResult<c extends Bit = Bit, s extends Bit = Bit> = {
carry_out: c;
sum: s;
};
// FullAddrMap[`${b1}${b2}${carry_in}`] -> AdderResult
type FullAddrMap = {
"000": AdderResult<0, 0>;
"001": AdderResult<0, 1>;
"010": AdderResult<0, 1>;
"011": AdderResult<1, 0>;
"100": AdderResult<0, 1>;
"101": AdderResult<1, 0>;
"110": AdderResult<1, 0>;
"111": AdderResult<1, 1>;
};
type FullAdder<
b1 extends Bit,
b2 extends Bit,
carry_in extends Bit
> = FullAddrMap[`${b1}${b2}${carry_in}`];かんたん!
これを繰り返せば筆算ができますね!全加算器を組み合わせて複数桁に対応したMultiFullAdder型を実装しました.なお,前回の型パズルで用いた型ハックによって ,TS2589による再帰回数制限を回避しています.また,前回作った自然数であるNatural型を使ってループインデックス等を実装しています.
最後に,桁溢れを起こさない加算演算子であるAddInt型を実装しました.普通の計算機では扱えるビット数が決まっているため,大きすぎる数を足すと桁があふれる場合もあります.一方,型の世界ではどんなに長い配列を使っても良いので溢れる必要がないのです.AddInt型はMultiFullAdderを使って足し算をしますが,桁が溢れた場合は1桁拡張された答えを返します.
また,例によって型のテストも同時進行で書いていきます.
// 112233445566778899 + 123456789123456789 = 235690234690235688
// prettier-ignore
assert<
IsExact<
AddInt<
[0,0,0,0,1,0,0,0,0,1,1,1,0,0,0,0,1,0,1,1,0,1,1,1,0,1,1,1,1,0,1,0,1,0,0,1,1,1,0,1,1,1,0,1,1,1,0,1,0,1,1,1,0,0,0,1,1,0],
[0,0,0,0,1,0,0,0,1,1,1,1,1,0,1,0,0,0,0,0,1,0,1,1,0,0,1,1,0,1,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,0,0,1,0,1,1,0,1,1,0,1,1,0]
>,
[0,0,0,0,0,1,0,0,1,0,1,1,0,1,1,0,1,0,1,1,1,1,0,1,1,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,1,0,1,0,1,0,1,0,1,0,0,0,1,0,1,1]
>
>(true);そこそこ大きな数も足せていますね.これで自然数の足し算ができるようになりました.
引き算
2進数の引き算は2の補数を使った足し算で実現できるので,案外簡単に実装できました.ある数の2の補数を計算するComplement型を作り,SubInt型を実装しました.
掛け算,割り算
掛け算や割り算については,コンピュータ内部でどのように処理されているのか知らなかったので調べてみました.こちらの回答によれば,まさに私達が普段行っている筆算と同じアルゴリズムで計算をしているようです.よく考えれば,2進数だって同じ位取り記数法を利用しているのですから,計算方法が似るのも当たり前ですよね.
というわけで,小学校で習った掛け算と割り算の筆算を思い出しながら愚直に実装し,乗算を計算するMultiUint型と除算および剰余を計算するDivideAndModUint型ができました.また,その過程で自然数を大小比較するCompareUint型や,ビットシフトを行うRightShift型とLeftShift型も作りました.
自然数ユーティリティ
最終的には計算結果を"1.41421356"のように文字列で表示する予定です.そのために,自然数を文字列に変換するUintToStr型をこのタイミングで実装しました.ついでに,文字列を自然数に変換するStrToUint型も作りました.
2進数 ↔10進数の変換は一見して難しそうですが,今や我々は自然数の四則演算,剰余演算,大小比較,ビットシフトを自由に行えるので無敵です.余裕で実装できてしまいました.
Step 3:実数の表現を定義する
実数の表現は,IEEE 754を参考に定義します…とかっこよく言ってみましたが,要はいつもどおり符号部,仮数部,指数部で実数を表しますよ,ということです.浮動小数点数Float型を以下のように定義しました.ただし,今後の実装を簡単にするため,以下の部分は一般的な表現とは異なります.
- 10を基数とする
- 仮数部の桁の重みは自然数のときと同じ
- そのために,指数部をと解釈し,とする
// float number = (is_negative ? -1 : 1) * fraction * 10^(-1 * exponent)
export type Float = {
fraction: Bits;
exponent: Natural;
is_negative: boolean;
};Step 4:実数の四則演算を実装する
自然数の四則演算はすでにできているので,符号と指数部にだけ気をつければいいですね.
足し算と引き算
まずは符号を考慮せず,指数部だけを考えて足し算してみましょう.例えば,が次のように表されているとします.
このままでは2数の指数部が違うので仮数部をそのまま計算できません.この場合,の指数部を減らす方向で調整すれば精度が落ちずに済むので,
としてから仮数部を足すことでが得られます.というわけで,2数の指数部を一致させるMatchAndExpandFloatsExponent型を作り,符号を考慮しないで加算するAddUfloat型を実装しました.減算に関しても同様にSubUfloat型を実装しました.
次に符号の影響を考えると,
というパターンがあるとわかります.これは2数の符号によって適切にAddUfloat / SubUfloatすればいいだけなので条件分岐でどうにかなりますね.というわけで符号を考慮して実数を加算 / 減算するAddFloat型 / SubFloat型を実装しました.
掛け算
掛け算は簡単ですね.仮数部はそのまま乗算すればよく,指数部は2数のものを足し合わせればよく,符号部はXOR的なかんじでパーペキです.実例を見るのが早いですね.
と計算できます.MultiFloat型を実装しました.
割り算
符号部に関しては掛け算のときと同じです.
一方,指数部に関しては,どのように処理すれば良いのかパッと思いつきませんでした.実数の割り算が出来ないとあっては,「小学生からやり直せ」と言われても仕方ありません.
というわけで,こちらの5年生「小数のわり算」というサイトを参考に勉強しなおしました.こちらのサイトによれば,

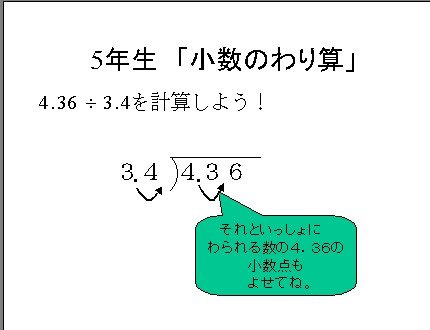
「割る数の指数部を増やしながら,それが0になるまで割られる数の仮数部を10倍せよ」
と読めます.やってみます.
お,できた.神サイトじゃん.
おかげさまで無事DivideFloat型が実装できました.
実数ユーティリティ
計算結果を文字列として表示するために,実数を文字列に変換するFloatToStr型を実装しました.前に実装したUintToStrを使ってfractionを文字列にし,あとは適切に小数点"."や"0"といった文字を追加しています.
なお,StrToFloatは実装しませんでした.なんとなく面倒だったのと,別にfloat型を手書きするのは大変じゃないので.
Step 5:平方根の近似アルゴリズムを実装する
実数の四則演算ができるようになりましたので,それらを使って平方根を近似するアルゴリズムを実装しましょう.ここではニュートン法を使います.
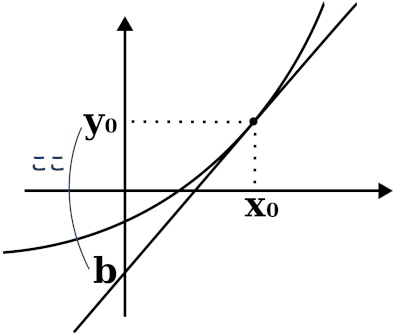
ニュートン法はとした時のを反復的に近似するアルゴリズムです.(つまりと軸の交点の座標をがんばって求めるということですね.)このアルゴリズムの根本的な部分は,接線を使っての近似値をどんどん目的の値に近づけることです.下の図のように,近似値から,より目的の値に近い値を繰り返し計算するわけです.近似値の初期値は適当に取ればいいですね.なーるほど.
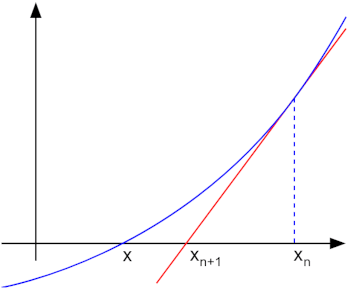
今回は,定数()についてを求めたいとします.の漸化式(からを求める式)の導出は,文章が長くなってしまったので畳んでおきますが,最終的に次のようになりました.
漸化式の導出
数学に長らく触れていないので不安しかありませんが,ノーヒントでがんばります.よろしくおねがいします.求めたい値をとおくと,
となるので,としてを解けば良いですね.
次に,上の点における接線を求めます.もろもろの公式は忘れてしまいましたが,ともかく,求める式は傾きと切片で次のような形になるはずです.
傾きに関してはですね.切片は,「から切片までの長さ」がわかればなんとかなりそうです.
この長さは,となります.これは,傾きがであることを考えれば自明ですね.これをから引けば切片です.
というわけで,
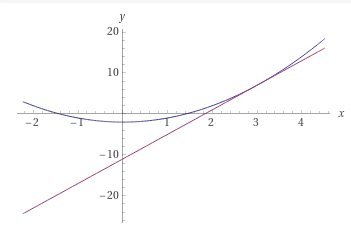
となりました.ほんまか?としてグラフを描いてみましょう.
出典: WolframAlpha
おーできてそうですね.
ここまで来ればもうひといきです.と軸との交点が次の,つまりになりますので,
となります.これを一般化すると,
となって,漸化式を求められました.
※なお,式をもう少しいじってともできたのですが,こうすると割り算を最初に計算することとなり,実装上では精度が落ちてしまうのでやめました.
この漸化式を実装したNewtonSqrtStep型がこちらです.
type Two = {
fraction: [0, 1];
exponent: [];
is_negative: false;
};
type NewtonSqrtStep<
current_value extends Float,
squared extends Float
> = DivideFloat<
AddFloat<MultiFloat<current_value, current_value>, squared>,
MultiFloat<current_value, Two>
> extends infer A
? Cast<A, Float>
: never;current_valueは現在の近似値,squaredは2乗された値,つまりのことです.これらを与えると,NewtonSqrtStepはより近似された値を返します.
で…できた….ここまで長かった….
完成!実際に計算してみよう
としてを計算してみましょう.
type squared_value = {
fraction: RemoveExtraZerosBits<StrToUint<"2">>;
exponent: NumberToNatural<0>;
is_negative: false;
};
type initial_value = {
fraction: RemoveExtraZerosBits<StrToUint<"20">>;
exponent: NumberToNatural<1>;
is_negative: false;
};
type result1 = NewtonSqrtStep<initial_value, squared_value>;
type result2 = NewtonSqrtStep<result1, squared_value>;
type result3_tmp1 = NewtonSqrtStep<result2, squared_value>;
type result3_tmp2 = ShrinkFloatExponentOneDigit<result3_tmp1>;
type result3_tmp3 = ShrinkFloatExponentOneDigit<result3_tmp2>;
type result3 = RemoveExtraZerosFloat<result3_tmp3>;
type result4_tmp1 = NewtonSqrtStep<result3, squared_value>;
type result4 = RemoveExtraZerosFloat<result4_tmp1>;
const result: FloatToStr<result4> = null;※いろいろ謎の型が登場しているのは気にしないでください.
ShrinkFloatExponentOneDigitやRemoveExtraZerosFloatといった型は,近似値の精度や仮数部の表現を調整しているだけです.こうすることでTS2589を回避しつつできるだけ精度を出しています.
「え,前回の型ハックで無限再帰できるようになったんじゃないの?」
と思われるかもしれませんが,実は,TS2589は再帰回数だけではなく型のインスタンス化回数も制限していて…という話は長くなるので割愛します.TypeScriptの型で遊ぶ時、再帰制限を無効化するを参考にするか,tsc.jsを読みましょう.ちなみに,ループを使わずにNewtonSqrtStepを何度も呼んでいるのもTS2589回避のためです.
上記のコードを実行すると…
〜15.690秒後〜
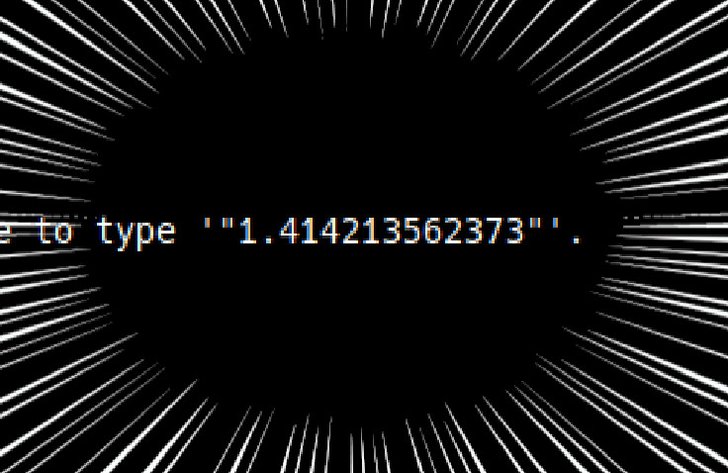
src/index/sqrt2.ts:33:7 - error TS2322: Type 'null' is not assignable to type '"1.414213562373"'.
33 const result: FloatToStr<result4> = null;
~~~~~~
Found 1 error.一夜一夜に人見頃(ひとよひとよにひとみごろ)…その先を知りません.
Wolfram Alpha君に確認してみます.
result: 1.414213562373(型で計算したほう)
actual: 1.41421356237309... (Wolfram Alphaの結果)完全に一致!
だけじゃもったいないので,も計算してみましょう!をちょこっと変えればいいだけです.
ちなみに,の覚え方は「人並みに奢れや女子(ひとなみにおごれやおなご)」です.ツイッターに書いたら暖かくなりそうな内容ですが,ともかく計算してみます.
result: 1.732050807569
actual: 1.73205080756887...いいですね!最後の桁が違っていますが,近似誤差でしょう.(それに8よりも9のほうが近いし)
までの自明でないをすべて求めてみました.
# sqrt(5):富士山麓鸚鵡鳴く(ふじさんろくおうむなく)
result: 2.23606797750
actual: 2.2360679774997...
# sqrt(6):ツヨシ串焼くな(つよしくしやくな)、煮よ良く弱く(によよくよわく)
result: 2.44948974278
actual: 2.4494897427831...
# sqrt(7):菜 (7) に虫来ない((な)にむしこない)、「菜に虫いない」とも。
result: 2.64575131106
actual: 2.6457513110645...
# sqrt(8):ニヤニヤ呼ぶな(にやにやよぶな)
result: 2.8284271247
actual: 2.828427124746...
# sqrt(10):父 (10) さん一郎兄さん((とう)さんいちろうにいさん)
result: 3.1622776604
actual: 3.162277660168...語呂合わせの出典: 平方根 - Wikipedia
まとめ
TSの型システムだけを使ってを計算できました.最終的にはニュートン法を用いて解を2次収束で近似するという複雑な処理をしましたが,もとをたどってみれば,あの単純な全加算器がすべての計算を担っているのです.そう考えると,とてもロマンがありませんか?(問いかけ)ありますよね?(同調圧力)
反省点として,「自然数表現に10進数を使ったほうが実装も楽だったし計算速度も早かったのでは?」とか「ビット数を可変長にしないほうがもっときれいに実装できたのでは?」などがありますが,些細なことです.だって2進数のほうがかっこいいじゃん.可変長のほうが,ロマンがあるじゃん.もともと趣味のコードなんてロマン駆動開発なんだから.
今回の実装に使ったテクニックが業務に役立つことは一生ありませんが,「掛け算とか割り算って計算機内部ではどうなっているんだろう」とか「そもそも 計算 って何なんだろう」などと考える良いきっかけになりました.今回の型パズルで,我々は実数の四則演算を自由に行えるようになりました.次は虚数か,はたまた四元数か.夢が広がりますね.
コラム(蛇足)
本記事のアイキャッチとして使ったこちらの画像は,
Blenderで1時間くらいかけて作りました.「TSでパズルします」というのがひと目でわかるので気に入っています.
このパズルのパターンは,Jigsaw puzzle generatorを使用して作成しました.そのため,ピースはそれぞれ異なる形であり,本物のパズルとして遊べるようになっています.TSのロゴはシンプルな見た目なので,ジグソーパズルとして普通に難しそうですね.