ざっくりホーア論理

2024/09/28

階乗を計算する関数があります。

const fact = (n) => {
  let x = n;
  let y = 1;
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  return y;
};

console.log(fact(5)); // 120

この関数が正しく動くことをホーア論理でざっくり証明します。そのための1つの方法は、関数の各時点で成り立つ条件を、コメントとして書いていくことです。

例えば、returnの直前ではyの中身がnの階乗になっていてほしいです。なので以下のように書きます。

const fact = (n) => {
  let x = n;
  let y = 1;
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }  return y;
};

今回は簡単のために、このプログラミング言語で扱える値は0以上の整数だけと仮定します。

そうすると、nの階乗はいつでも計算できます。したがって、関数の先頭で必要な条件は特にありません。

ここでは{ True }と書いておきましょう。常に成り立つアサーションassert(true)があるようなイメージです。

const fact = (n) => {
  // { True }  let x = n;
  let y = 1;
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

次にわかりやすいのは、冒頭の2つの代入文の後の条件です。xの値がn、yの値が1になっていてほしいです。

const fact = (n) => {
  // { True }
  let x = n;
  let y = 1;
  // { x = n かつ y = 1 }  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

ここで、1ステップ前、つまりlet y = 1;の実行前には、どんな条件が成り立てば良いかを考えます。

let y = 1;という代入文は、実行するとyを1に上書きします。なので、「実行後の条件で、すべてのyを1に戻した条件」が、実行前にも成り立てば良さそうです。したがって以下のようになります。

const fact = (n) => {
  // { True }
  let x = n;
  // { x = n かつ 1 = 1 }  let y = 1;
  // { x = n かつ y = 1 }
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

同様に、let x = n;の実行前は以下のようになります。

const fact = (n) => {
  // { True }
  // { n = n かつ 1 = 1 }  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

ここで、2つの条件が連続していることに注目します。

// { True }
// { n = n かつ 1 = 1 }

2つの条件が連続しているときは、前の行の条件を仮定したときに、後の行の条件が成り立てばOKです。

今回の例だと、Trueを仮定したときに（つまり無条件で）n = n かつ 1 = 1が成り立つのでOKです。

このことを

// { True }
// ->
// { n = n かつ 1 = 1 }

と書くことにしましょう。->は「ならば」と読みます。

const fact = (n) => {
  // { True }
  // ->  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

次に、ループの前、途中、後で常に成り立つ条件、ループ不変条件（Loop invariant）を考えます。

今回のループ不変条件は、y * x! = n!です。

ループを進めるにしたがって、yは増加し、xは減少していきます。これらをうまいこと組み合わせると、お互いでバランスをとって一定になるといった感じです。

まず、ループの前で不変条件が成り立つことを確認します。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // { y * x! = n! }  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

ここで、x = n かつ y = 1を仮定すると、y * x! = n!は、1 * n! = n!となるので確かに成り立っています。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->  // { y * x! = n! }
  while (x !== 0) {
    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

次に、ループのBodyの先頭で成り立つ条件を考えます。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // ここで成り立つ条件を考える    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

とりあえず、ループの1回目でここに入ってきた場合を考えてみましょう。まず、変数の状態はループ前から変化していないので、不変条件が成り立ちます。加えて、ここに入ってきたということはx !== 0が真であったということですから、xが0でないことも成り立ちます。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }    y = y * x;
    x = x - 1;
  }
  // { y = n! }
  return y;
};

ここで、ループのBodyの末尾でも不変条件が成り立つことを示したいです。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    y = y * x;
    x = x - 1;
    // ここでも{ y * x! = n! }が成り立ってほしい  }
  // { y = n! }
  return y;
};

なぜなら、1回目以降も不変条件が成り立つ（保存される）ことを示せるからです。ある回のBodyの先頭で不変条件が成り立つことは、その前回のBodyの末尾で不変条件が成り立つことから言えます。

というわけで、Bodyの末尾に不変条件を書いて、それが成り立つことを確認します。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    y = y * x;
    x = x - 1;
    // { y * x! = n! }  }
  // { y = n! }
  return y;
};

直前は代入文なので、先程と同じように実行後の条件のxをx - 1に戻します。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    y = y * x;
    // { y * (x - 1)! = n! }    x = x - 1;
    // { y * x! = n! }
  }
  // { y = n! }
  return y;
};

さらに、yをy * xに戻します。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    // { (y * x) * (x - 1)! = n! }    y = y * x;
    // { y * (x - 1)! = n! }
    x = x - 1;
    // { y * x! = n! }
  }
  // { y = n! }
  return y;
};

条件が2つ連続しているので、前者を仮定して後者が言えるか確かめます。

// { y * x! = n! かつ x != 0 }
// ->
// { y * (x * (x - 1)!) = n! }
// ->
// { (y * x) * (x - 1)! = n! }

大丈夫そうですね。

x! = x * (x - 1)!の変形がポイントです。例えば5! = 5 * 4! = 5 * (4 * 3 * 2 * 1)みたいな感じです。

注意したいのは、x != 0という仮定のおかげで(x - 1)!と書けるということです。この仮定がないと、xは0であるかもしれず、それだと-1の階乗が出てきてしまうのでダメです。

さて、ループの前でも、途中でも不変条件が成り立つ（保存される）ので、ループの後でも成り立つと言えます。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    // ->
    // { y * (x * (x - 1)!) = n! }
    // ->
    // { (y * x) * (x - 1)! = n! }
    y = y * x;
    // { y * (x - 1)! = n! }
    x = x - 1;
    // { y * x! = n! }
  }
  // { y * x! = n! }  // { y = n! }
  return y;
};

さらに、ループを抜けたということはx !== 0が偽であったということなので、追加で以下のようになります。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    // ->
    // { y * (x * (x - 1)!) = n! }
    // ->
    // { (y * x) * (x - 1)! = n! }
    y = y * x;
    // { y * (x - 1)! = n! }
    x = x - 1;
    // { y * x! = n! }
  }
  // { y * x! = n! かつ !(x != 0) }  // { y = n! }
  return y;
};

条件が連続しているので、前者を仮定して後者を示します。

// { y * x! = n! かつ !(x != 0) }
// ->
// { y * x! = n! かつ x = 0 }
// ->
// { y * 0! = n! }
// ->
// { y * 1 = n! }
// ->
// { y = n! }

というわけでこの関数では、Trueを仮定し（つまり無条件で）、returnの直前まで実行されたならば、y = n!が成り立っています。

これで証明完了です。

const fact = (n) => {
  // { True }
  // ->
  // { n = n かつ 1 = 1 }
  let x = n;
  // { x = n かつ 1 = 1 }
  let y = 1;
  // { x = n かつ y = 1 }
  // ->
  // { y * x! = n! }
  while (x !== 0) {
    // { y * x! = n! かつ x != 0 }
    // ->
    // { y * (x * (x - 1)!) = n! }
    // ->
    // { (y * x) * (x - 1)! = n! }
    y = y * x;
    // { y * (x - 1)! = n! }
    x = x - 1;
    // { y * x! = n! }
  }
  // { y * x! = n! かつ !(x != 0) }
  // ->
  // { y * x! = n! かつ x = 0 }
  // ->
  // { y * 0! = n! }
  // ->
  // { y * 1 = n! }
  // ->
  // { y = n! }
  return y;
};

形式化

この関数はあらゆる入力に対して正しく振る舞うことが示されたので、すぐにリリースできます。テスト工程は必要ありません。

いやいや、式変形や場合分けに間違いがあるかもしれないじゃないか！

貴様の頭の中でやった証明など信用ならん！！

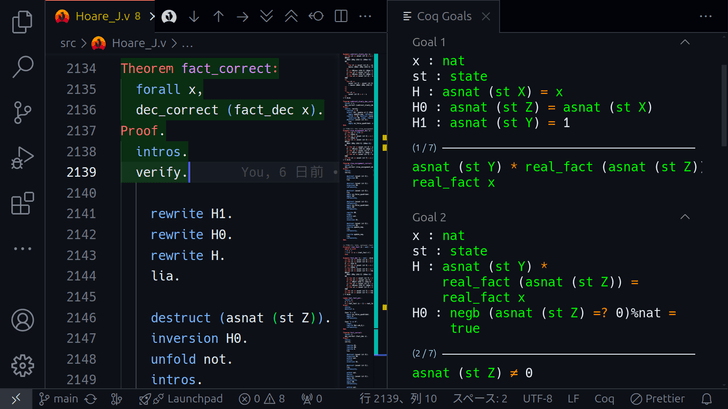
という方には、Coqをおすすめします。以下は、今回のプログラムをCoqで形式化し、証明しているところです。

今回のプログラムをCoqで証明しているところ

右に表示されてるのが示すべき条件で、その示し方を左に書いた命令（タクティク）で指示しています。

式変形や場合分けはCoqがやってくれます。また、簡単な部分については自動で解決してくれます。

UATはCoqのチェックが通ることを確認したら完了ですね（？）

まぁ一方で形式化のコストがかかるんですけれども

まとめ

なぜかホーア論理をざっくり勉強したので、備忘のために階乗の関数をざっくり証明しました。

プログラムはメモリの状態を次々に変化させます。それらの状態で成り立つ条件を追いかけることで、最終的に示したい性質が導かれることを確認しました。

今回取り上げたのはホーア論理のさわりの部分だけです。

この考え方を発展させていくことで、より多くのプログラム、例えばポインタを使ったプログラムなどに対しても証明を与えられるのだそうです。

すごいですね

参考文献

続けて読む…

TypeScriptの型で全加算器から浮動小数点数，そして√2

2021/06/07

SICPの備忘録

2023/07/29

Zコンビネータを思いつきたい

2024/01/22

Advent of Code 2021攻略ガイド

2021/12/28

「クロージャは関数と環境のペア」とは？（JavaScript）

2023/12/02

ラムダ計算で型のリハビリ

2024/02/20

書いた人

sititou70のアイコン画像
sititou70

都内の社会人エンジニア4年生。Web技術、3DCG、映像制作が好き。