よわよわエンジニアがTAPL（型システム入門）を読んだら

こんにちは，sititou70です．私は社会人2年目のよわよわWebフロントエンドエンジニアであり，「数学」とか「証明」とは無縁の人生を送っています．

そんな私ですが，がんばって型システム入門（通称：TAPL）という本を読み終えました．全32章，503ページ，牛乳パック1本分の重さがあり， 自立します． 自立する本は大抵やばいです．

TAPLの序文を見ると，想定読者は

1. プログラミング言語と型理論を専門とする大学院生および研究者
2. プログラミング言語の鍵となる概念に触れたい，計算機科学の全分野の大学院生および習熟度の高い学部生¹

となっています．本記事では

「そんな本を，学生や専門家でない人間（私）が読んだらどうなるのか」

について書きます．専門的な用語は避けますので，TAPLの雰囲気だけでも感じ取ってもらえたら嬉しいです．

どうなったのか

• 宇宙語が読めるようになった
• 「型安全」を説明できるようになった
• 用語を慎重に使うようになった
• 型システムの「表現力」についてなんとなくわかった
• 数学とプログラミングの関係がなんとなくわかった
• 型システム入門できた
• こぼれ話
• まとめ

宇宙語が読めるようになった

TAPLには 規則図 と呼ばれる図が数ページごとに登場します．ちょっと見てみてください

？？？

これらの図は，ぱっと見の意味不明さから 宇宙語 と呼ばれています．²しかし，TAPLの議論はこの図をベースに進んで行くので，なんとか頑張って理解しました．

規則図とは，あるプログラミング言語³の定義を，なんと 全て 表したものです．定義というのは，例えば以下のようなものです．

• プログラムをどのように表現するか（構文形式）
• プログラムがどのように計算されるか（評価規則，スモールステップ意味論）
• プログラムにどのような型がつくか（型付け規則）

（※簡単のために，この記事では「項」のことを「プログラム」と表現しています）

先ほど見た規則図もまた，１つのプログラミング言語を表しています．さすがに本格的なシステム開発などは難しいですが，例えばリストを定義して多相的なソート関数が書けるほどの能力があります．

これだけのものを図1枚で表そうとしているので， 専用の記法で表現を圧縮しまくった結果，宇宙語になっちゃった みたいなかんじです．

「型安全」を説明できるようになった

私に 娘（6歳）⁴ がいると仮定します．⁵

TAPLを読む前だと

娘「ねぇパパ， 型安全 ってな〜に？」

ワイ「ファッ！？いきなりどうしたんや，娘ちゃん？」

娘「 型安全 って，今までいろんなところで聞いたことのある言葉だけど」

ワイ「（6歳やろ！どこで聞いたんや！）」

娘「よく考えたら具体的になんなのかわからなくて……」

ワイ「な，なるほどなぁ……」

ワイ「あ……あれやろ？int型の変数に文字列をつっこもうとしたら怒られるから安全とかいう……」

娘「ふーん」

娘「じゃあ例えば，Javaでは変数宣言時に型を指定するから，Javaは型安全ってこと？」

ワイ「え！？ま，まぁそういうことになるんやない……？」

娘「Perlでは型を書かないから，型安全でない？」

ワイ「た……たぶんそうやない？」

娘「……ホント？」

ワイ「ふえぇ……」

TAPLにおける型安全の定義

「型安全」という言葉はコンテキストによっていろいろな意味で使われ，専門家の間でも見解が分かれるみたいです．

しかし，少なくともTAPLでは 「進行と保存が成り立つこと」 と定義されています．

• 進行定理：正しく型付けされたプログラムは，別の形に（1ステップ）評価できるか，値である
• 保存定理：プログラムを評価しても型付けは変化しない

もう少し簡単に言うと，型安全性とは「正しく型が付けられたプログラムを評価していって停止するならそれは値である」または「型が付けられたプログラムはおかしくなることがない」性質です．

専門家たちは，プログラミング言語の定義（規則図）上で，進行と保存が ありうる全てのプログラムに対して 成り立つことを証明し，その体系の型安全性を示します．これにより，「〇〇言語は型安全 / 型安全でない」といえるわけです．

TAPLが難しいと言われる理由の1つが，この 証明作業 です．定理やら命題やら補題やら何やらが 例の宇宙語ベースで 展開されていくので，1行読み進めるのに数十分かかることもありました．

TAPLを読んだ後なら

娘「ねぇパパ， 型安全 ってな〜に？」

ワイ「おお！それは 進行と保存が成り立つこと やで！プログラムが おかしくならない ことを保証できるんや！」

ワイ「これはHarperさん，Wrightさん，Felleisenさんなど，えらい頭の良い人たちが考えたんや」

ワイ「ただし，型によってどこまでの おかしなこと を抑制できるのかは言語によるからな！より高度な検査には相応の表現力のある型システムが必要になるけど，それだけ言語機能との兼ね合いが難しくなるし，証明や型検査器の実装も大変になんねん」

娘「なるほど，型システムは言語設計とも深い関係にあって，両者は手を取り合って設計を進めるべき⁶なんだね！」

娘「ちなみにJavaとPerlは型安全なの？」⁷

ワイ「よっしゃ宇宙語もってこい！構造的帰納法で証明したるわ！」⁸

用語を慎重に使うようになった

TAPLを読むまでは，危険とされる言語機能を使わないことや，型検査の範囲を広げることを型安全と言っていた気がします．例えば，

「TypeScriptを書くときは 型安全なコードを心がけましょう！ 」

といった発言です．

ここまで読まれた皆様なら，上記に違和感を感じたと思います．TAPLでいう型安全性とは，各プログラミング言語の仕様から証明できる，またはできないものであって，プログラムの書き方とは無関係だからです．

TAPLを読むことで，1つの用語は複数の意味で使われる場合があるとわかりました．「TAPLの定義が正しくて，ほかは誤りだ！」と言いたいのではありません．その場の状況において，より伝わりやすく，誤解のない言葉選びが重要だと考えます．

TAPLで強化された知識や語彙が，そのことに役立てばいいなと思っています．

型システムの「表現力」についてわかるようになった

Twitterを見ていると， 「〇〇型システムはつよい」 とか 「☓☓ 型システムは △△ に比べたらよわよわ」 といった発言を見かけます．

私も小学生のころは 「どの漫画のキャラが最強か」 という議論を友人と繰り広げたりしたものですが，話しているうちに 「結局……"強さ"って何？」 という哲学的な疑問に落ち着くのでした．

同じような疑問を型に対しても持っていたわけですが，TAPLを読むことで「型システムの強さとは， 表現力 のことである」とか，「表現力の高い型システムは より多くのプログラムが おかしくならないのを保証できる」と理解しました．

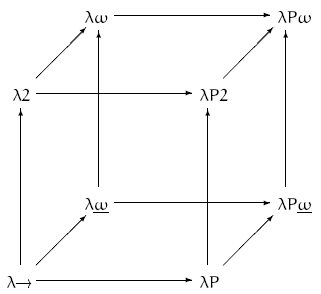
ラムダキューブ

以下の図は ラムダキューブ と呼ばれ， いろいろな型システムの関係を示す地図 のようなものです．これは「表現力」を理解するのにも役立ちます．

出典: Lambda cube.png, ウィキメディア・コモンズより，以降同じ図に関して出典略

この立方体を理解する鍵は「〇〇から □□ を作る機能」⁹であると思います．ここに登場する型システムは，以下のような機能を持っていたり，持っていなかったりします．

• プログラム ¹⁰ から プログラム を作る機能
• 型 から プログラム を作る機能
• 型 から 型 を作る機能
• プログラム から 型 を作る機能

1つずつ説明させてください．

プログラム から プログラム を作る機能

これは 関数 のことです．例えば

function plusOne(x) {
  return x + 1;
}

という関数plusOneですが，コイツに1というプログラムを与えれば1 + 1というプログラムを作れるし，2を与えれば2 + 1が作れます．プログラムからプログラムを作れています．

ラムダキューブの手前左下にある ${\lambda}{\rightarrow}$ へ注目してください．

${\lambda}{\rightarrow}$ がこのキューブの 原点 で，一番 よわい 表現力を持つ型システムです．なんと，この世界には「関数型」 しか ありません（！）

（この計算体系では，値は関数だけで， 真偽値，整数，配列すら無い というのですからびっくりです．さらにびっくりなのは，そんな世界でも 関数だけで真偽値，整数，配列などが作れる という事実です．¹¹頭のいい人が考えることはぶっ飛んでますね？）

型 から プログラム を作る機能

これは，Javaの ジェネリクス が例として分かりやすいと思います．例えば以下のコードでは

var list = new ArrayList<Integer>();
list.add(1);

ArrayListにIntegerという型を与えることで，整数を格納できる配列（のプログラム）を作っています．つまり，型からプログラムを作れています．

先程の原点 ${\lambda}{\rightarrow}$ から上に移動して， ${\lambda}{2}$ を見つけてください．

ラムダキューブの矢印は，矢印の 先 の型システムが， 根 のシステムを拡張して定義されることを表します．

${\lambda}{2}$ は， ${\lambda}{\rightarrow}$ の機能に 加えて ，ジェネリクスに相当する¹²「全称型」という機能を持っています．

したがって， ${\lambda}{2}$ は ${\lambda}{\rightarrow}$ よりも つよい 表現力を持つといえるのです．

型 から 型 を作る機能

いくつかのプログラミング言語では， 型を受け取って型を返す 関数を定義できます．

Haskellをご存知の方は 型コンストラクタ というものが対応するそうですが，私は Haskellなにもわからない ので説明できませんごめんなさい．

TypeScriptをご存知の方は次の例を見てください．

type Pair<T> = [T, T];
type Numbers = Pair<number>;
// Numbersは[number, number]型

Pairにnumber型を与えて[number, number]型を作っています．つまり，型から型を作っています．

このような機能は「型演算子」と呼ばれています．

${\lambda}{\rightarrow}$ から奥に行った ${\lambda}{\underline{\omega}}$ は，${\lambda}{\rightarrow}$ の機能に加えて型演算子も持っています．

プログラム から 型 を作る機能

Q. プログラムから型を作る機能ってなに？

A. わ　わかんないっピ…

――

――――

――――――

この機能は 依存型 と呼ばれているんだっピ

だけど依存型は，TAPLでも発展的内容として深く触れないんだっピ…

うわさだと，依存型によって 「配列の範囲外アクセスを型レベルで抑止」 したり， 「配列がソートされていることを型レベルで検証」 できたりするそうなんだっピ¹³

すごいっピね！

${\lambda}{\rightarrow}$ から右に行った ${\lambda}{P}$ は，${\lambda}{\rightarrow}$ の機能に加えて依存型も持っているんだっピ！

ラムダキューブまとめ

ラムダキューブでは ${\lambda}{\rightarrow}$ が原点であり，一番弱い表現力を持つのでした．

対象的に，全ての矢印が向かう先である ${\lambda}{P\omega}$ は， Calculus of Constructions とも呼ばれ，上述の全ての機能を持つ最強の型システムです．（Coq のもとになった型システムだそうです）

しかし，型システムの冒険は終わりません．

例えば，このキューブの外にある型システム（まだ見ぬ強敵）や，それらとラムダキューブを統一してしまう 「純粋型システム」 なる仕組み（超裏ボス）もあったりするのだそうです．

インフレ具合がバトル漫画並なんだよな．

数学とプログラミングの関係がなんとなくわかった

私はTAPLを読むまで，

「型 ってプログラミング界隈の概念でしょ？」

と思っていました．

しかしTAPLを読むと，

型システムは，1900年代初頭，Russellのパラドックスなど，数学の基礎を揺るがした論理的パラドックスを回避する手段として，最初に形式化された

とあります．FORTRANの考案が1953年とされているので，それよりだいぶ前の話です．

つまり， もともと数学や論理学で発明された型理論という概念が，後になってプログラミングに活かされた のだとわかります．

Russellのパラドックス

みなさんは「Russellのパラドックス」という言葉を聞いたことがあるでしょうか．

Russellのパラドックスとは，すごくざっくりと説明すると（すごくざっくりとしか説明できない）

Russellさん「あーちょっと暇だし，¹⁴ 自分自身を要素として含まない集合全体の集合 でも考えてみるか〜」

Russellさん「は？その集合に自分が含まれるかどうかが 矛盾するやんけ！ こりゃ数学を基礎から揺るがす大事件やで！」

Russellさん「……よく考えたら， こんな変な集合を定義できるほうがおかしいわ 」

Russellさん「せや！ 型 ¹⁵ を導入することで文法に制限を加え，変な集合を定義できなくしたろ！」

〜型理論の基礎誕生〜

みたいな感じですたぶん．

プログラミングに数学は必要？

Russellさんの事件などが発端となって，論理学では様々な仕組みが整備され， おかしなこと が起こりにくくなりました．

驚くべきことに，論理学と先ほど紹介したラムダキューブの各体系は精密に対応することがわかっており，これをカリー＝ハワード同型対応といいます． 正直意味はよくわかっていない のですが，なんだか声に出したくなるかっこよさがありますね（？）

つまるところ，論理学で おかしなこと が起こりにくくなったので，それに対応するプログラミングにおいても おかしなこと が起こりにくくなったということみたいです．論理学の発展が，私達の快適なプログラミングを支えているのです．

「プログラミングに数学は必要か？」

というのは，特に私のような初学者が感じがちな疑問です．これに自分自身で答えるなら

「数学を知らなくてもプログラミングができる場合はある¹⁶けど，それは数学のおかげ」

となるでしょうか．

もちろん，これはプログラミングが数学から恩恵を受けている一例に過ぎません．

頭のいい人たちに感謝ですね．

型システム入門できた

ある日のことでした．

――――――

――――

――

ワイ「……」（TAPLを読んでいる）

ワイ「ハァーーわからん！なんやねんこの定義！絶対おかしいやろ誤植ちゃうか！？」

ワイ「エラッタには……載ってない！こうなったら元の論文あたって確認したる！」

ワイ「（元論文を読んで）TAPLとおんなじこと書いとる……そりゃまぁワイが間違っとるか……」

ワイ「あれ？ワイ，型理論の論文をなんとなく読めてないか……？」

――

――――

――――――

ということがあったのです．開いた論文にもTAPLと同じ宇宙語が使われていたので，なんとなーく雰囲気で目的の箇所を探せました．英語の技術ドキュメントでも，コードの部分だけはふんわり読めるあの感覚です．

これって結構すごくないですか？数ヶ月前まで全くの素人だったヤツが，（内容の難易度はともかく）ちゃんとした論文を読んでいるのです！

あっ、これが……

型システム入門 ってコト！？（タイトル回収）

こぼれ話

おわりに

せっかくTAPLを読んだので読書感想文でも書こうと思い，筆を（キーボードを？）執りました．また，単なる感想文ではなく「『型システム入門』入門」としても読めるように意識してみました．

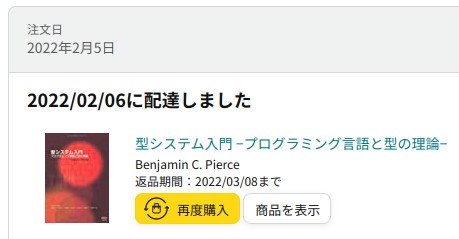
ところで，Amazonの注文履歴を見ると

とありますので，TAPLの読了には約3ヶ月かかったことになります．そりゃ全32章と長いですからね……．

長いということは，それだけここに書ききれなかった話題があるわけです．例えば，「コンパクトな規則だけでJavaのコア機能が構成できるFJ！すげぇ！」とか「数学的帰納法の双対概念？余帰納法ってなんやねん！」とか．

また，「読了」とは言っていますが，全ての内容を理解したかと聞かれると決してそんなことはなく……実際一部の理論は概形だけ掴んで飛ばしてしまいました¹⁷

したがって，本記事に間違っている部分があるかもしれません．もし発見された際には，是非マサカリを投げていただけると大変助かります．

それでは！

2022/07/04追記

依存型について追加で調べた記事を書きました