物の数は数え方によらないことを確認する【鳩の巣原理】
2024/10/20みなさんこんにちは。物、数えてますか?
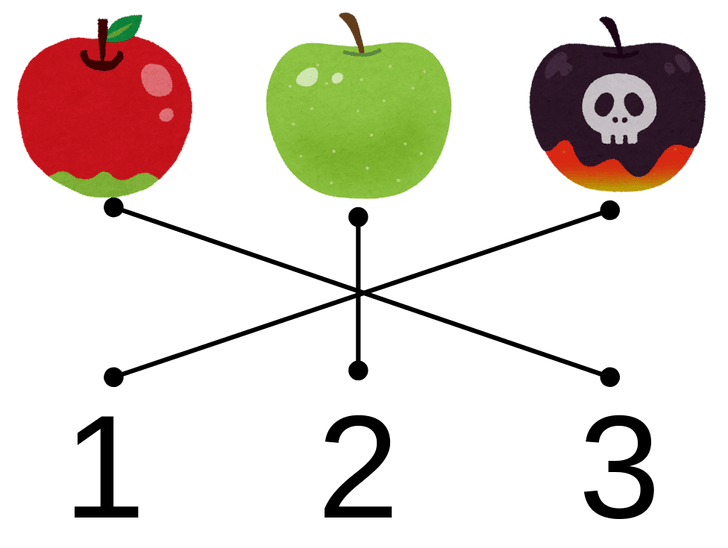
例えばここにりんごがいくつかあります。
左から右へ1、2、3と数えると、りんごが3つあるとわかります。
これは数学的には、りんごから集合 への全単射(1対1対応)を見つけたということになります。
しかし、全単射はこの1種類だけではありません。
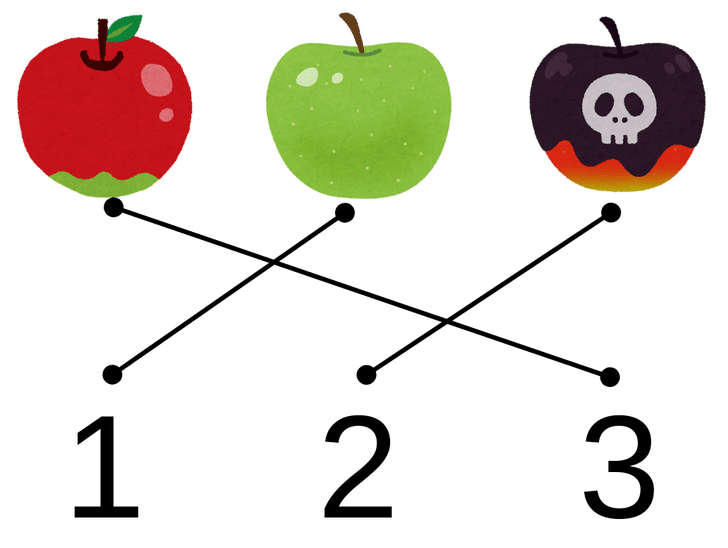
人によっては、右から左へ1、2、3と数えるかもしれません。
または、真ん中、右、左と数える人もいるかもですね。
一般に、n個のりんごについて 種類の全単射があります。どのような全単射でも(どのような数え方でも)りんごを正しく数えていると言えるのでしょうか?
つまり、 から への全単射を見つけたなら、 と言えるでしょうか?
今回はCoqでこれを示してみました。つまり背理法禁止です。
リポジトリ:https://github.com/sititou70/constructive-pigeonhole/tree/main
この記事では、証明の大まかな流れを紹介します。
ステップ1:鳩の巣原理を示す
鳩の巣原理とは、「 羽のハトが 個の巣に入っているとき、 ならば、複数のハトが入っている巣がある」というものです1。
当たり前に思えますが、ちゃんと示すにはハトの羽数 について帰納法を適用します。
0の場合
前提の が成り立たない(そんな自然数 はない)ので成り立ちます。
n + 1の場合
nで原理が成り立つことを仮定して、n + 1でも成り立つことを示します。
一番最後のハトが入る巣について、同じ巣に入る他のハトがいるかどうかによって場合分けします2。
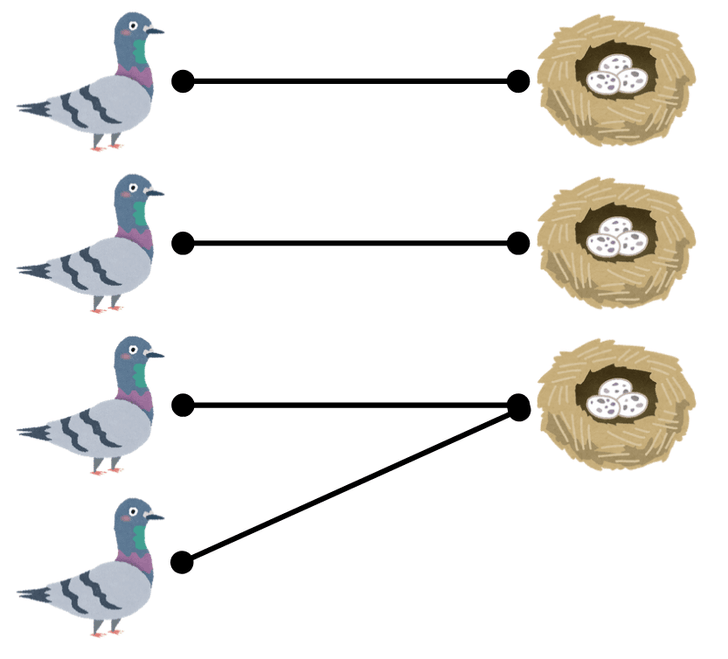
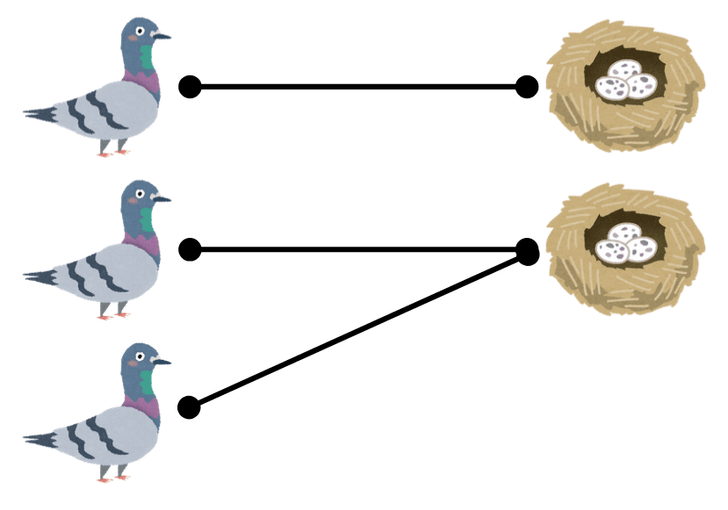
同じ巣に入る他のハトがいる場合
以下のような状況です。
この場合、一番最後のハトと同じ巣に入るハトがいるので、原理は成り立ちます。
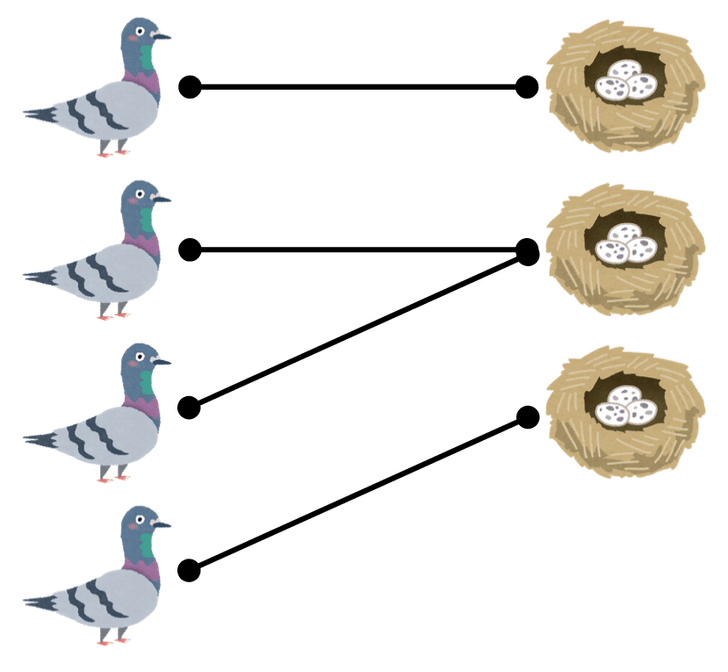
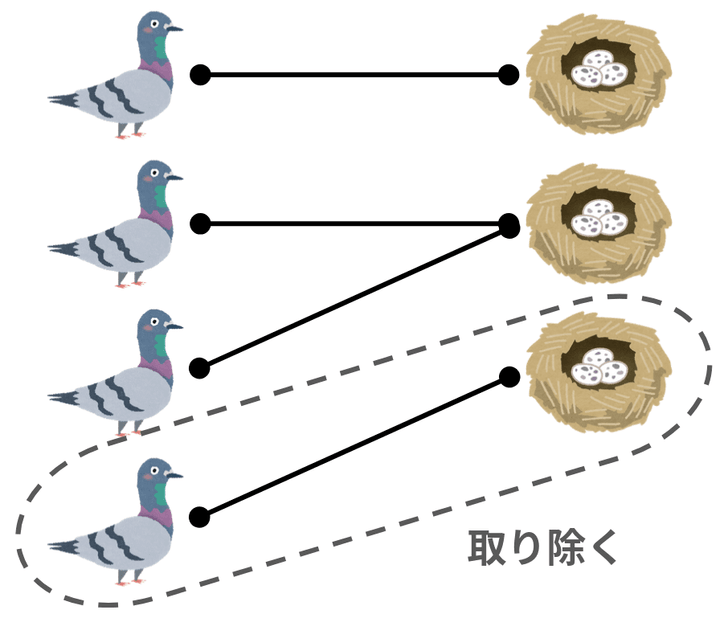
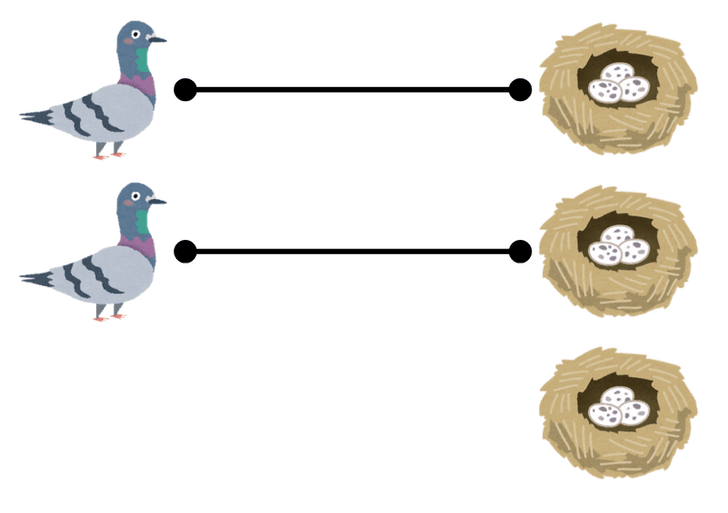
同じ巣に入る他のハトがいない場合
以下のような状況です。
この場合は、一番最後のハトと、対応する巣を取り除きます。
そうすると、残った 羽のハトに対して帰納法の仮定より原理を適用できます。
結局、のこりのなかで複数のハトの入る巣が見つかるので、原理が示されました。
ステップ2:鳩の巣原理の変形版を示す
鳩の巣原理の変形版とは、「 羽のハトが 個の巣に入っているとき、 ならば、ハトが入っていない巣がある」というものです。
当たり前に思えますが、ちゃんと示すにはハトの羽数 について帰納法を適用します。
0の場合
なので、ハトはいませんが巣は1つ以上あります。例えば最初の巣にはハトが入っていないため成り立ちます。
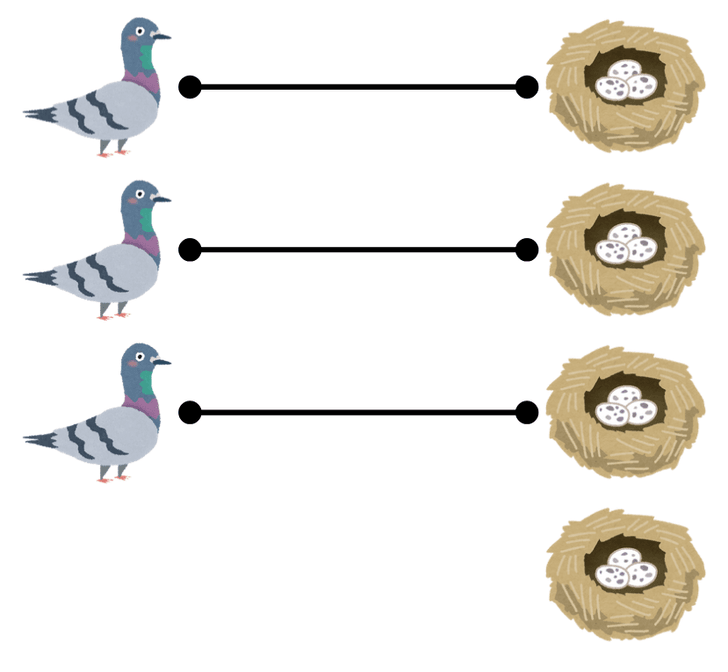
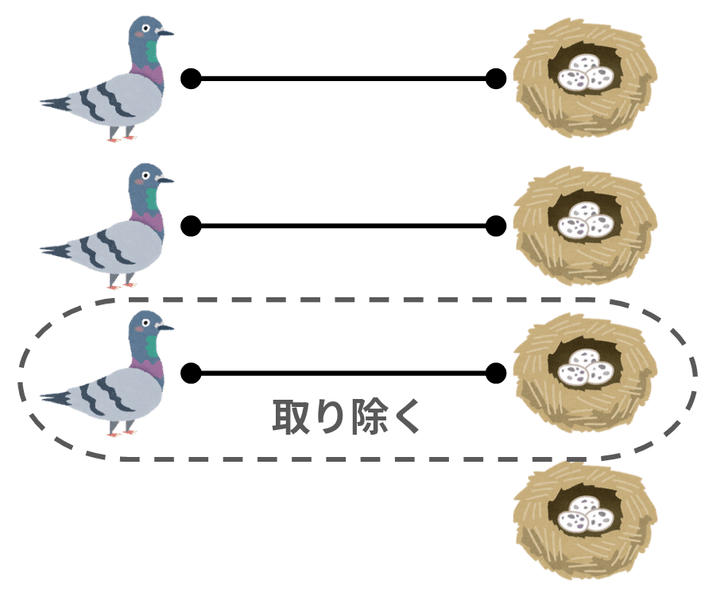
n + 1の場合
最後のハトと対応する巣を取り除きます。もしその巣に入っている他のハトがいる場合は、適当に最初の巣に入れます。
そうすると、残った 羽のハトに対して帰納法の仮定より原理を適用できます。
結局、のこりのなかでハトの入っていない巣が見つかるので原理が示されました。
ステップ3:物の数は数え方によらないことを示す
いま、 羽のハトが 個の巣に入っているとします。
鳩の巣原理とその変形版から、それぞれ以下が言えます。
- ならば、複数のハトが入っている巣がある。
- ならば、ハトが入っていない巣がある。
それぞれの対偶を取ります。
- 複数のハトが入っている巣がない、ならば
- ハトが入っていない巣がない、ならば
ここで、「複数のハトが入っている巣がない」とは単射のことで、「ハトが入っていない巣がない」とは全射のことです。なので
- ハトから巣への単射が存在するならば
- ハトから巣への全射が存在するならば
したがって2つを組み合わせると
「ハトから巣への単射が存在し、かつ全射が存在する」ならば「 かつ 」
となって、
ハトから巣への全単射が存在するならば
が示せました!
なのでより一般的に、 から への全単射を見つけたなら、 と言えます。
まとめ
お疲れ様でした。
私達は物を数えるとき、無意識のうちに対象から自然数への全単射(1対1対応)を探しています。
そして、鳩の巣原理とその変形版を示すことで、全単射の取り方によらず物が数えられることがわかりました。鳩の巣原理は、物の数を数えるという基本的なことの、さらに基礎になっているようです。
鳩の巣原理は、一見すると自明に思えます。「ハトの数が巣の数より多いんだから当たり前じゃん」といった感じです。
しかし「新井敏康、鳩はどこへ行った?」によれば、
結局,鳩の巣原理を,集合の要素の個数の大小を比較することによって自明であるとするのは,集合の要素の個数そのものが鳩の巣原理によって決まるので,循環していると考えられる.
とのことです。
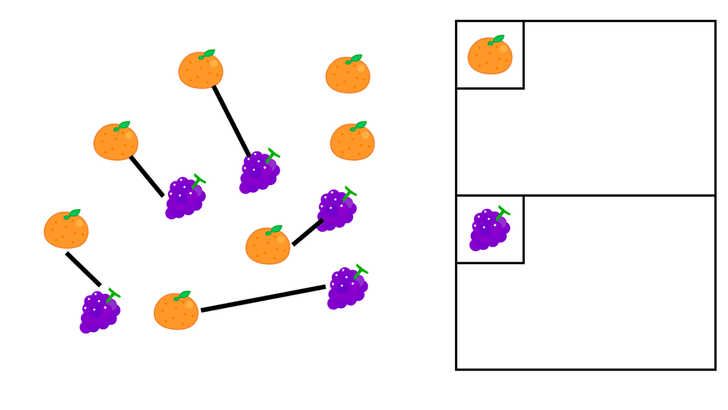
そういえば、小学校の算数の授業で、みかんとぶどうを線で対応させてどちらの数が多いか、または同じ数かというのをやった気がします。
出典:【小学校受験】 数の多少(1対1対応)問題を徹底解説!解き方のポイント・家庭での教え方
こんな時期から、全単射、1対1対応という概念が登場していたんですね。小学校で習うような内容であっても、実は突き詰めていくと奥が深いんだなぁと感じます。
私はこういう分野にはまったく詳しくないのですが、おもしろかったので紹介しました。あと、Coqで書いた証明の内容を忘れないうちに書いておきたかったのもあります。
ありがとうございました。
参考文献
フリー画像の出典
- https://www.irasutoya.com/2012/11/blog-post.html
- https://www.irasutoya.com/2014/10/blog-post_718.html
- https://www.irasutoya.com/2018/11/blog-post_498.html
- https://www.irasutoya.com/2013/04/blog-post_2929.html
- https://www.irasutoya.com/2014/07/blog-post_4435.html
- pigeonholeを鳩の巣とするのは誤訳であり、単なる仕切り箱や分類箱の意味ではないかという説があります。しかし、実際のハトと考えたほうが可愛いので、ここではそうします。↩
- この場合分けは帰納法によって示せます。↩