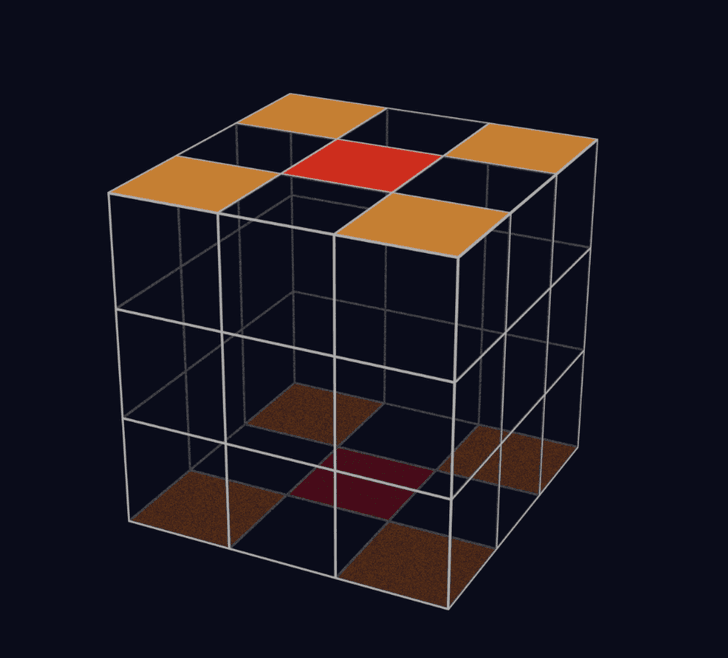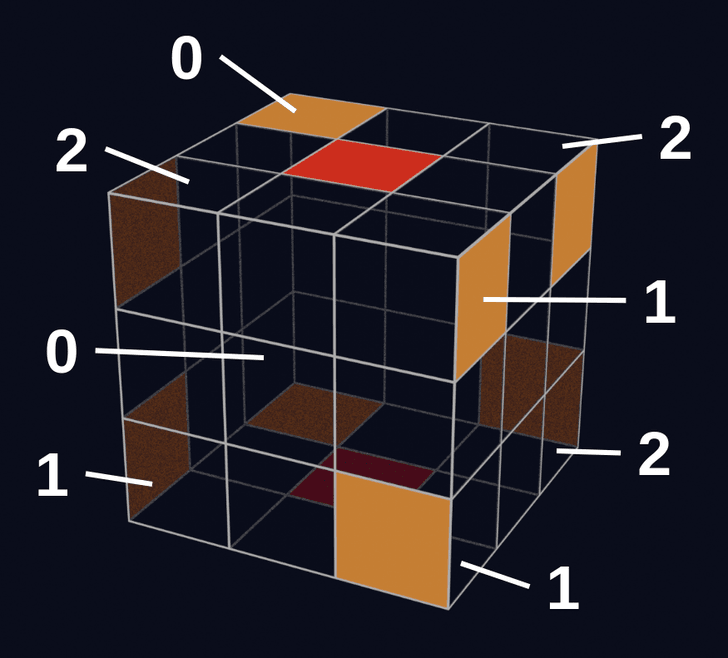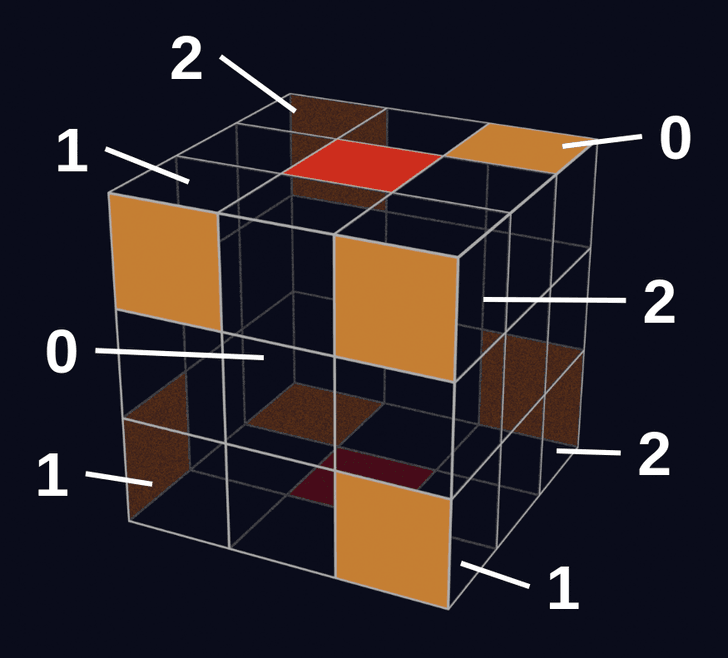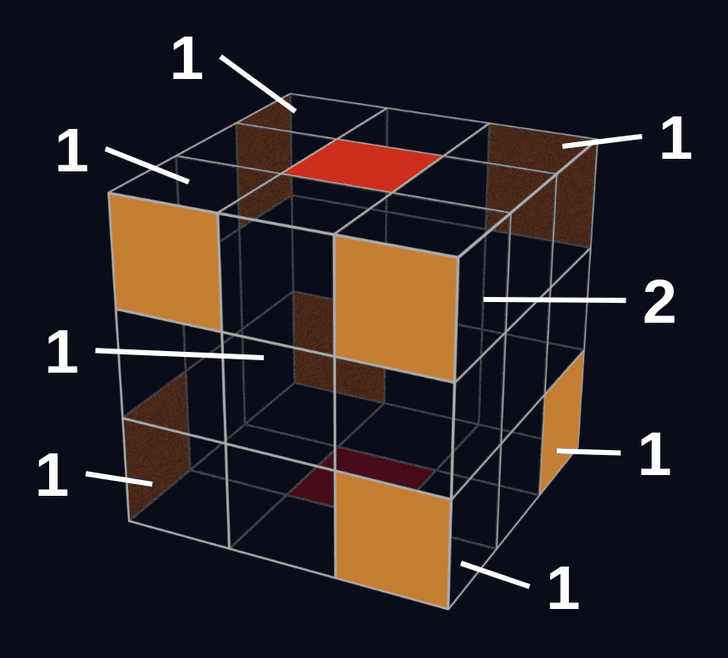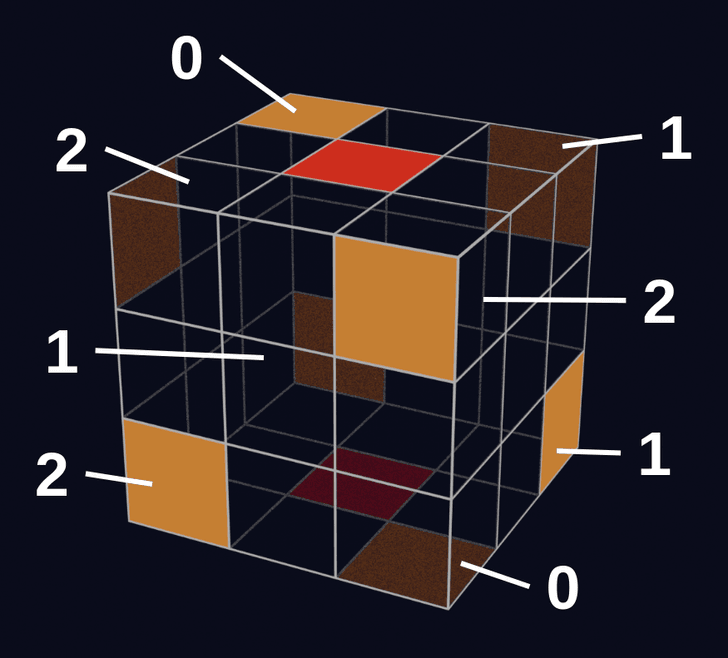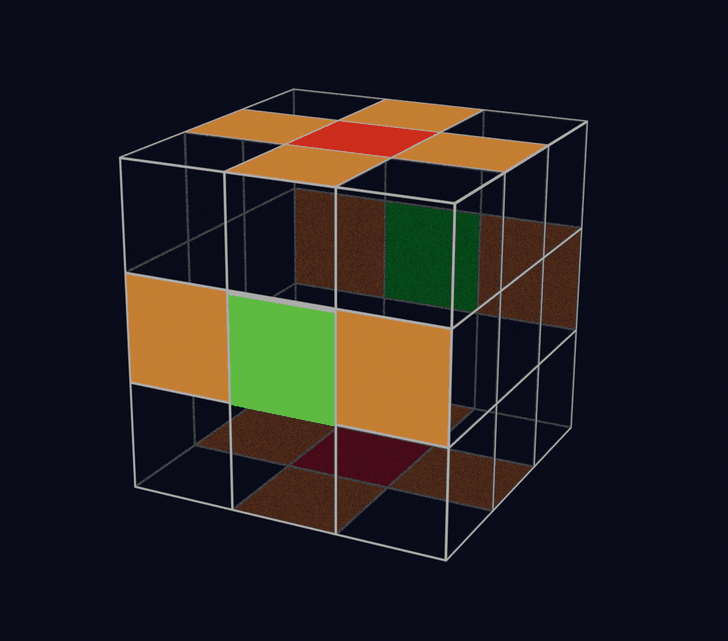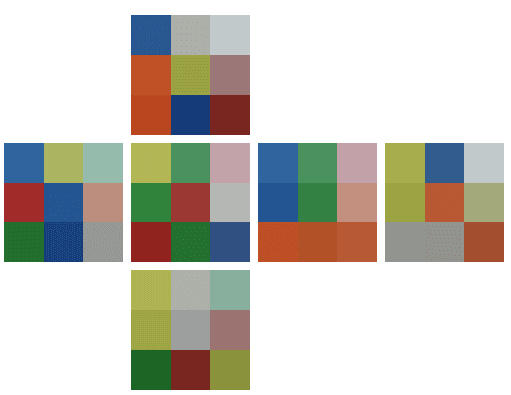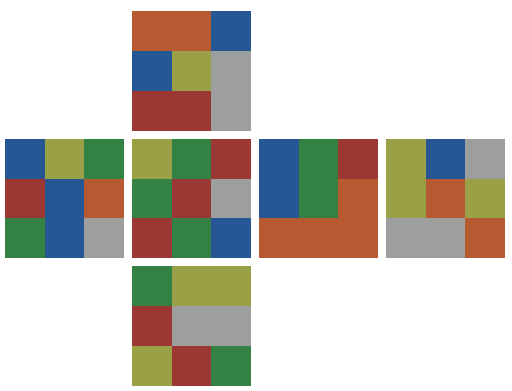解けないキューブ仙人への道
2025/02/25以前の記事では、ルービックキューブが解けるかどうかを、異常なパーツがあることや、正常なパーツの過不足で判定しました。
今回の記事では、たとえ正常なパーツのみで構成されたキューブであっても、解けない場合があることを説明します。また、キューブをスキャンして解けるかどうかを判定するプログラムも作ります。
パーツの名前(センターキューブ、エッジキューブ、コーナーキューブ)の定義については、以前の記事を参照してください。
面の名前(F面、R面、U面など)の定義や、回転記号の定義は、TORIBOによる解説を参照ください。
理論編
コーナーキューブの回転量に関する制約
コーナーキューブの回転量の合計が3の倍数でないと、そのキューブは解けません。
回転量の定義
コーナーキューブの回転量を定義します。
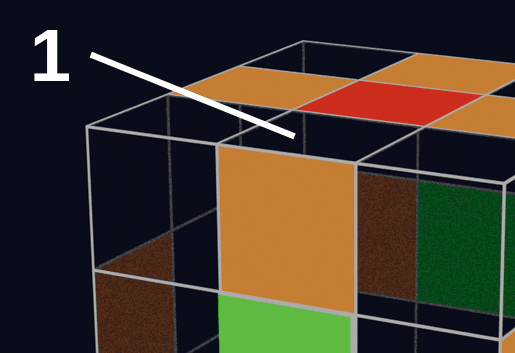
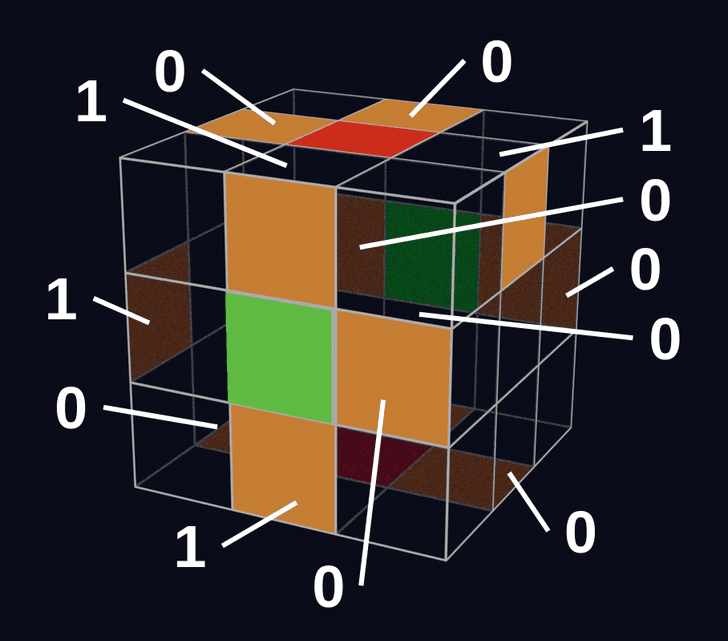
定義1:「コーナーキューブの基準方向」は、そのコーナーキューブが属しているU面またはD面の方向。(図の赤で示した面の方向)
定義2:「コーナーキューブの基準面」は、揃っている状態のコーナーキューブについて、基準方向と同じ方向の面。(図のオレンジ色の面)
定義3:「コーナーキューブの回転量」は、基準方向から基準面が時計回りに回転している回数。
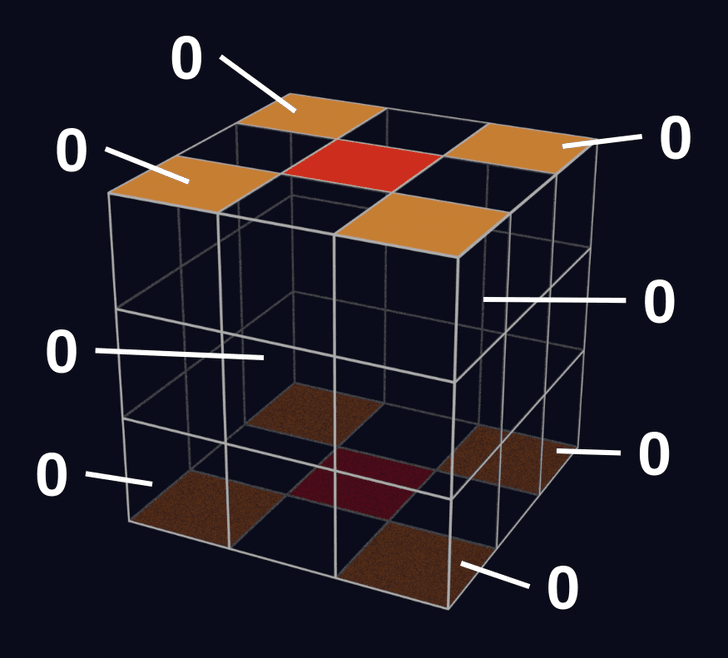
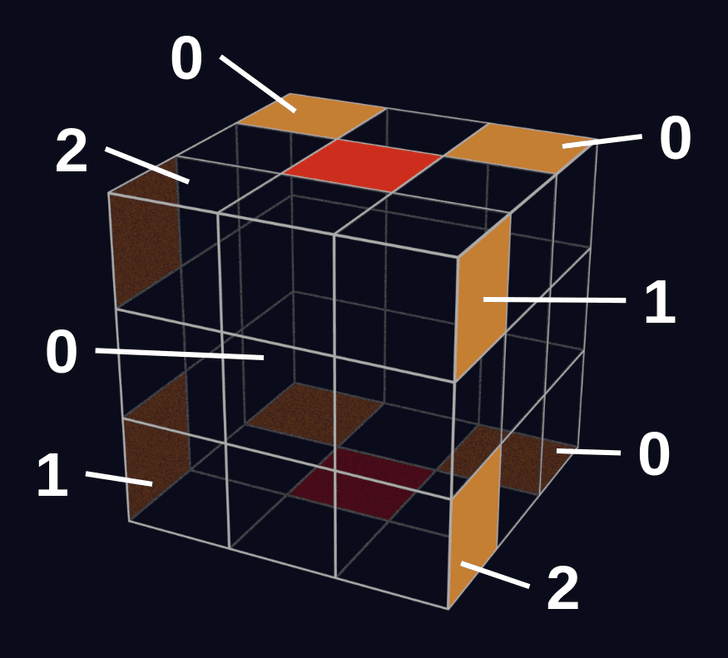
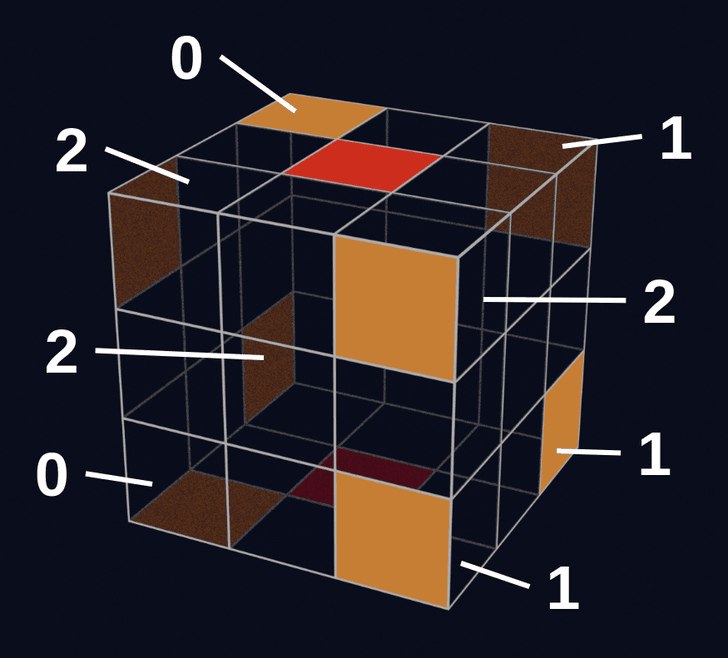
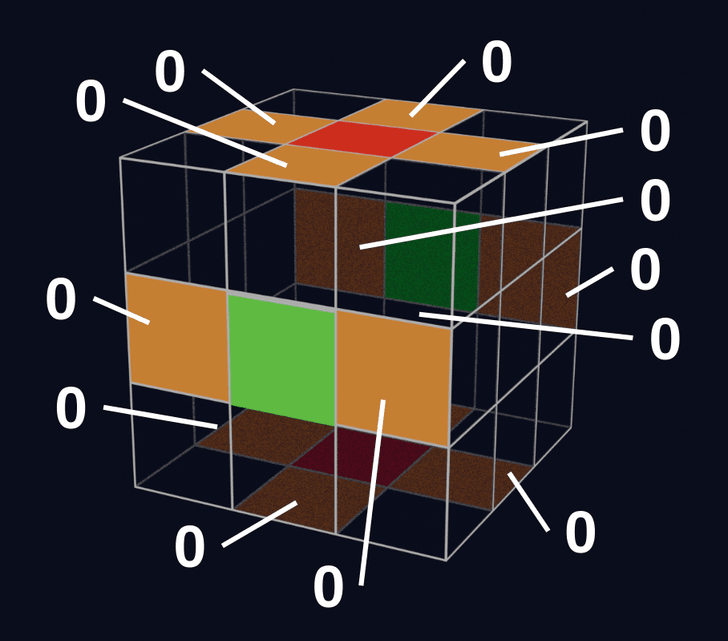
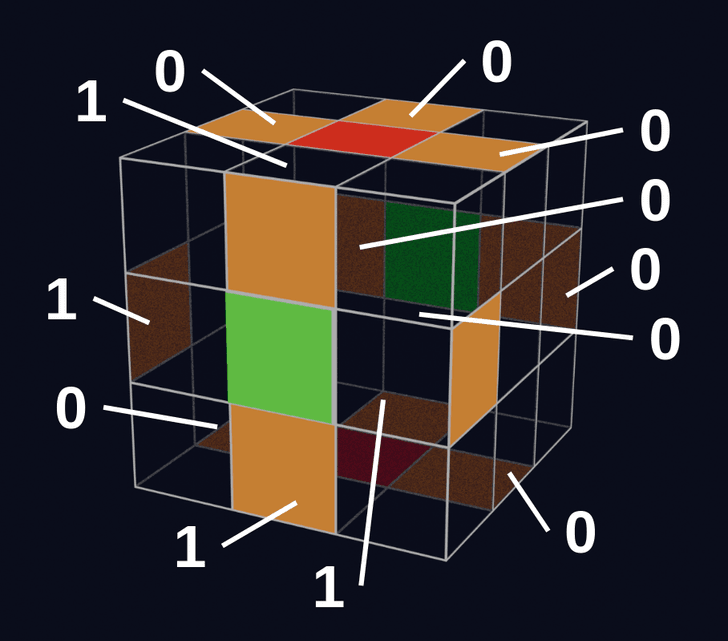
例えば、U面の一番手前のコーナーキューブに関して、回転量が0、1、2のときの状態は以下のとおりです。
回転量の合計が3の倍数でないと解けない
コーナーキューブの回転量の合計は、キューブを操作しても3の倍数に保たれます。証明は割愛しますが、コーナーキューブの位置と回転、キューブの各操作について、すべてのパターンを確認すれば良いです。
ここでは、揃っている状態からキューブを動かしてみて、回転量の変化を観察してみます。
初期状態では、回転量の合計は0で、これは3の倍数です。
次にFをしてみると、
回転量の合計は6になって、これは3の倍数です。
次にRをしてみると、
回転量の合計は9になって、これは3の倍数です。
次にUをしてみると、
回転量の合計は9になって、これは3の倍数です。1
次にBをしてみると、
回転量の合計は9になって、これは3の倍数です。
次にLをしてみると、
回転量の合計は9になって、これは3の倍数です。
次にDをしてみると、
回転量の合計は9になって、これは3の倍数です。2
結局、揃っている状態からキューブをどのように動かしていっても、回転量の合計は3の倍数になりそうなことがわかりました。
なので、回転量の合計が3の倍数でなければ、それは揃っている状態から動かしていったものではないということになるので、「解けない状態」であるとわかります。
エッジキューブの回転量に関する制約
エッジキューブの回転量の合計が2の倍数でないと、そのキューブは解けません。
回転量の定義
コーナーキューブのときと同じように、回転量を定義していきます。ただ、こちらの定義の方が少し複雑です。
定義1:「エッジキューブの基準方向」は、そのエッジキューブがU面またはD面に属していればその方向、そうでなければ属しているF面またはB面の方向。(図の赤色の面に属していればその方向、そうでなければ属している緑色の面の方向)
定義2:「エッジキューブの基準面」は、揃っている状態のエッジキューブについて、基準方向と同じ方向の面。(図のオレンジ色の面)
定義3:「エッジキューブの回転量」は、基準方向から基準面が時計回りに回転している回数。
例えば、U面の一番手前のエッジキューブに関して、回転量が0、1のときの状態は以下のとおりです。
回転量の合計が2の倍数でないと解けない
エッジキューブの回転量の合計は、キューブを操作しても2の倍数に保たれます。証明は割愛しますが、エッジキューブの位置と回転、キューブの各操作について、すべてのパターンを確認すれば良いです。
ここでは、揃っている状態からキューブを動かしてみて、回転量の変化を観察してみます。
初期状態では、回転量の合計は0で、これは2の倍数です。
次にFをしてみると、
回転量の合計は4になって、これは2の倍数です。
次にRをしてみると、
回転量の合計は4になって、これは2の倍数です。3
次にUをしてみると、
回転量の合計は4になって、これは2の倍数です。
次にBをしてみると、
回転量の合計は8になって、これは2の倍数です。
次にLをしてみると、
回転量の合計は8になって、これは2の倍数です。4
次にDをしてみると、
回転量の合計は8になって、これは2の倍数です。
というわけで、揃っている状態からキューブをどのように動かしていっても、回転量の合計は2の倍数になりそうなことがわかりました。
なので、回転量の合計が2の倍数でなければ、それは揃っている状態から動かしていったものではないということになるので、「解けない状態」であるとわかります。
パーツの位置に関する制約
キューブのパーツ位置の置換は、偶置換で実現されなければなりません。
お勉強タイム
置換(並べ替え)の性質について学びましょう。5
長くなってしまったので、証明などは適当に読み飛ばしてください。
定義1:置換とは、対象の並べ替え方である。
例:
[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に並べ替えるのは置換です。
定義2:互換とは、2つの要素だけを入れ替える置換である。
例:
[1, 2, 3, 4, 5]を[2, 1, 3, 4, 5]に並べ替えるのは互換です。
定理1:あらゆる置換は、互換の連続で実現できる。
例:
[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に並べ替えるのは、以下のように互換操作の連続によって実現できます。縦の棒は、上下の要素が入れ替わっていることを表しています。
[1, 2, 3, 4, 5]
| |
[4, 2, 3, 1, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2]証明:
古典的なソートアルゴリズムは、互換の連続によってあらゆる状態の配列をソートできます。したがって、その逆の手順を行うことで、任意の置換が実現できるとわかります。
例えば、[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に、互換の連続によって置換したいとします。それは、[4, 3, 5, 1, 2]をバブルソートやクイックソートなどでソートし、その逆の手順を行えば実現できます。
性質1:置換を互換の連続で実現する方法は、一意ではない。
例:
[1, 2, 3]を[3, 1, 2]に置換する場合、
[1, 2, 3]
| |
[3, 2, 1]
| |
[3, 1, 2]のようにする方法と、
[1, 2, 3]
| |
[1, 3, 2]
| |
[3, 1, 2]のようにする方法があります。
ソートアルゴリズムが複数あることを考えると自明ですね。
定義3:idとは、何もしない置換である。
例:
[1, 2, 3, 4, 5]をidで置換すると[1, 2, 3, 4, 5]になります。
補題1:奇数個の互換の連続は、idにならない。
例:
[1, 2, 3, 4, 5]の任意の2つの要素を奇数回入れ替えて、もとの[1, 2, 3, 4, 5]に戻すことはできません。
証明:
例として、要素が5つの場合を考えます。
まず、配列の各位置の値を表すx[0]〜x[4]の変数を導入します。
配列: [1, 2, 3, 4, 5]
x[0]: 1
x[1]: 2
x[2]: 3
x[3]: 4
x[4]: 5次に、この証明だけで使用する2項演算子 を以下のように定義します。(このsは、サイン(正負の符号)の気持ち)
ここで、以下の積の値を考えます。
この積の値は、互換を行うたびに正負が反転します。いま、x[i]とx[j]の要素を入れ替える場合を考えます。
を評価している、それぞれのカッコについて、
- 中身の2つの変数が、どちらも入れ替え対象であるものは正負が反転します。
- について、入れ替え後は なので正負が反転します。
- 中身の2つの変数が、どちらも入れ替え対象でないものは正負が変化しません。
- 入れ替え前後で変数の値が変わらないので
- 中身の2つの変数が、どちらかだけ入れ替え対象であるものについて、それらの積としての正負は変化しません。
- 中身の2つの変数の、入れ替え対象でない位置をkとおきます。
- の場合、
- のような積のペアが必ずあります。
- 入れ替え後は になります。
- これは積の順番が変わっているだけなので正負は変化しません。
- の場合、
- のような積のペアが必ずあります。
- 入れ替え後は になります。
- それぞれのカッコの中で正負が反転しますが、2つ掛け合わせるので全体としては変化しません。
- の場合、
- のような積のペアが必ずあります。
- 入れ替え後は になります。
- これは積の順番が変わっているだけなので正負は変化しません。
[1, 2, 3, 4, 5]では、この積の値は1です。ここから互換を奇数回行うと、積の値は-1になります。一方で、もとの並びに戻るには、積の値は1でなければなりません。なので、奇数個の互換の連続はidにならないといえます。
この話は任意の要素数に一般化できるので、もとの補題が示されました。
この積の値は置換の符号としても知られます。
定理2:置換が2通りの「互換の連続」で実現されるとき、それぞれの互換の数の偶奇は一致する。
例:
[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に並べ替えるのは、以下のように2通りの「互換の連続」によって実現できます。
[1, 2, 3, 4, 5]
| |
[4, 2, 3, 1, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2][1, 2, 3, 4, 5]
| |
[1, 2, 4, 3, 5]
| |
[1, 4, 2, 3, 5]
| |
[4, 1, 2, 3, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2]上では3回の互換で、下では5回の互換で実現できました。ここで、3と5はどちらも奇数なので偶奇が一致しています。
証明:
それぞれの互換の連続をA、Bとおきます。
ここで「Aの操作をして、Bの逆操作を行う」という新しい互換の連続をCとおくと、Cはidになるということに着目します。
先程の、[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に並べ替えた例で考えてみます。
まず[1, 2, 3, 4, 5]に1つ目の互換の連続(A)を適用すると以下のようになって、
[1, 2, 3, 4, 5]
| |
[4, 2, 3, 1, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2]続けて2つ目の互換の連続(B)の逆操作をすると、
[4, 3, 5, 1, 2]
| |
[4, 3, 2, 1, 5]
| |
[4, 1, 2, 3, 5]
| |
[1, 4, 2, 3, 5]
| |
[1, 2, 4, 3, 5]
| |
[1, 2, 3, 4, 5]もとの[1, 2, 3, 4, 5]にもどります。
つまり、2つをつなげた互換の連続であるCは、idということです、
[1, 2, 3, 4, 5]
| |
[4, 2, 3, 1, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2]
| |
[4, 3, 2, 1, 5]
| |
[4, 1, 2, 3, 5]
| |
[1, 4, 2, 3, 5]
| |
[1, 2, 4, 3, 5]
| |
[1, 2, 3, 4, 5]ここで、AとBの互換の数の偶奇によって、Cの互換の数を考えます。
| # | Aの互換の数 | Bの互換の数 | Cの互換の数 |
|---|---|---|---|
| 1 | 偶数 | 偶数 | 偶数 |
| 2 | 偶数 | 奇数 | 奇数 |
| 3 | 奇数 | 偶数 | 奇数 |
| 4 | 奇数 | 奇数 | 偶数 |
ケース2と3では、Cの互換の数は奇数になっています。補題1を考えるとCがidであるということに矛盾するので、これらのケースはありえません。
よってケース1と4しか成り立たず、AとBの互換の数の偶奇は一致します。
定義4:偶置換とは、偶数個の互換の連続で実現される置換である。奇置換とは、奇数個の互換の連続で実現される置換である。
例:
[1, 2, 3, 4, 5]を[4, 3, 5, 1, 2]に並べ替えるのは、以下のような奇数個の互換の連続で実現できるため奇置換です。
[1, 2, 3, 4, 5]
| |
[4, 2, 3, 1, 5]
| |
[4, 3, 2, 1, 5]
| |
[4, 3, 5, 1, 2]キューブの話に戻ると
これは、揃っている状態からUをやったところです。
コーナーキューブに着目すると、4箇所を巡回するような置換になっています。
これは奇置換です。
[1, 2, 3, 4]
| |
[4, 2, 3, 1]
| |
[4, 1, 3, 2]
| |
[4, 1, 2, 3]エッジキューブにも着目すると、これも4箇所を巡回する置換です。
これも奇置換です。
なので、Uによるパーツの位置の置換は、全体としては偶置換です。キューブの対称性から、これは他の操作(FとかRとかD'とか)についても同じです。
そして、キューブをどのように操作したとしても、全体の置換としては偶置換になります。
例えば、以下のようなスクランブルについて考えます。
U R' L U R U' B2 U2 R2 U' F2 U' F2 D2 R D2 F' D' B' R180度の操作を、90度2回の操作に展開すると以下のようになります。
U R' L U R U' B B U U R R U' F F U' F F D D R D D F' D' B' Rそして、それぞれの操作を互換の連続に展開すると以下のようになって、
(Uを実現する偶数個の互換) (R'を実現する偶数個の互換) ...全体としては結局、偶数個の互換によって実現されます。
したがって、パーツの位置は、揃っている状態から偶置換で実現できないといけません。そうでないなら、それは揃っている状態から操作していったものではないということになるので、「解けない状態」であるとわかります。
実装編
上記の理論を、理解の確認もかねて実装しようと思います。あるキューブの状態が解けるかどうかを判定するプログラムを作ります。
キューブをスキャンする
各パーツの位置や回転を地道に入力しても良いのですが、それはあまりに面倒なので、カメラとOpenCV.jsを使ってキューブをスキャンすることにします。
まず、ユーザーにキューブの6面それぞれを、マーカーに合わせて撮影してもらいます。
ここで撮影を楽にするために、面の向き(4方向)は特に気にせず、後からプログラムで補正することにします。
撮影されたマーカー内の色の平均を取得すると、以下のようになります。
カメラの性能や周りの環境によって、同じ面でも色味が異なっています。
ここから、これらを6種類に分類していきます。
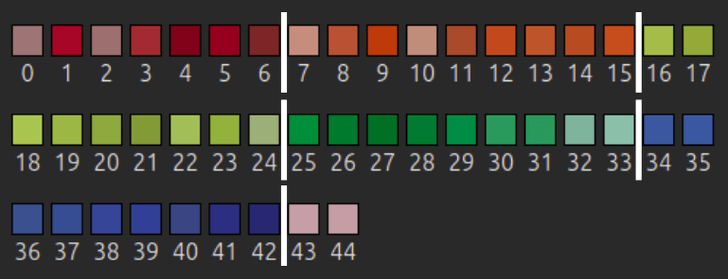
まず、これらの色をHSVに変換して、Saturationでソートすると以下のようになります。
先頭から9個取り出して、それらを白面であると認識します。なお、ここでセンターキューブがちょうど1つだけ含まれていない場合は読み取りエラーになります。
次に、残りの色をHueでソートします。
HSVでは、赤色はHueの0度と360度の境界にあります。
なので上記のソート結果では、赤色が配列の最初と最後をまたいでいます。
この赤色のまたぎ方は(またいでいないケースも含めると)9種類あるので、5つのクラスタを9回スライドさせながら、クラスタ内のHueの分散が最も小さくなるものを探索しました。
また、各クラスタ内にセンターキューブが1つだけ含まれていないものは除外します。条件に合うスライドが1つもないと読み取りエラーです。
今回の例で言えば、以下のスライドが最も良いです。
最後に、撮影時の各面の回転を補正します。
6面それぞれで4種類の回転が考えられるので、 パターンについて、パーツが正しいキューブ(以前の記事でやっていたこと)を探索し、最初に見つかったものを採用します。6 例によって、条件に合うパターンがないと読み取りエラーとします。
そうして得られたスキャン結果が以下です。
U面とD面の回転が補正されているのがわかります。
解けるかどうかの判定処理
回転量に関しては、マジで理論編の定義をそのまま実装しただけです。
置換に関しては、バブルソートを適当に実装して、互換の数を数えました。
デモ
2025年ではありえない画質で失礼します。
https://sititou70.github.io/cube-solvable-checker/
解けるキューブの条件
ここまでの解けない条件に一致しなければ、そのキューブは解けることが知られています。
それを証明するには、具体的なキューブの解法アルゴリズムを示せば良い気がしますが、それは他のサイトにまかせます。
正しいパーツで構成されたキューブの状態は、解けるかどうかを考慮しなければ 通りあります。12個のエッジキューブの配置と回転が 通りと 通りあって、8個のコーナーキューブの配置と回転についても同様だからです。
ここで、これらの状態を「エッジキューブ回転量の合計を2で割ったあまり」で分類すると、同数になることに気づきます。7
同様に、「コーナーキューブの回転量の合計を3で割ったあまり」と「偶置換と奇置換」で分類しても同数になるとわかります。
そして、コーナーキューブとエッジキューブの回転量、置換の偶奇性は独立して定まるので、解けるキューブの状態は 通りあるというわけです。
ルービックキューブのパターン数が約4,300京通りと言われるのはこういう理由だったんですね。
まとめ
本記事では、ルービックキューブが解けない条件を説明しました。そしてキューブが解ける条件まで到達したので、解けないキューブシリーズは今回で終了です。
しかし、群論としてのキューブの性質にはまだまだ続きがあります。
今回は群論につま先くらいまでしか入門していませんが、それでも置換の興味深い性質について理解できました。
気が向いたらさらに調べてみたいですね。
参考
- ルービックキューブを解く(その1:画像認識して解く)
- 色の扱いについて参考にさせていただきました。
- 一般に、Uでは回転量の合計は変化しません。↩
- おなじく、Dでも回転量の合計は変化しません。↩
- お察しの通り、Rではエッジキューブの回転量の合計は変化しません。↩
- 同様に、Lでも回転量の合計は変化しないです。↩
- 以下の記述は、簡単さを優先していて数学的に厳密ではないです。詳しくはWikipediaの置換(数学)を参照してください。↩
- 実態とは違う補正結果が得られることもありますが、十分にスクランブルされているならめったに起こりません。まぁ回転に気をつけて、展開図と同じになるように撮影すれば最悪問題ないのでこうしました。↩
- 具体的な証明は割愛しますが、エッジキューブを1つ選んで2通りの回転を考えると、それ以外のエッジキューブの向きが全く同じで、しかし全体としてのあまりは0と1であるペアが必ず見つかる……といったイメージです。↩