論理学と型システムへ同時に入門してみる

2026/01/24

純粋型システムを導入し、命題論理と単純型付きラムダ計算、述語論理とLogical Framework、二階述語論理と λP2\lambda P2 、高階述語論理とCalculus of Constructionsの対応を眺めてみます。

はじめに

以前から「論理学って結局なに？」という疑問がありました。

仕事では「論理的に説明しろ」とよく言われます。そのような方法の1つとして、新人研修では三段論法を教わりました。

しかし、それがどうして成り立つのかは説明されなかったので、いまいち納得できていない感もありました。

なので検索してみると、「正しい三段論法」と「誤った三段論法」があると出てきて、よりわからなくなりました。その正誤はどう見分ければ良いんですかね？　あと、真偽不明のビジネス系サイトとかも出てきて「インターネットの限界だ」となり、ちゃんとした本を買うことになりました。

ﾂｲｯﾀに生息する数学クラスタの発言を分析し、良さそうと判断したのが『論理学』 野矢茂樹（東京大学出版会）です。

ところで、論理とプログラミングには、カリー＝ハワード同型対応という深い関係があるそうです（唐突）

私は以前からプログラミングとか型システムについて興味があったので、「このへんを同時にやったらお得じゃね？」となりました。

この記事は、その際のノートをまとめたものです。

準備：ざっくりPTS入門

純粋型システム（PTS：pure type system）は、いろんな型システムを一般化したやつです。ちょっとパラメタを変えるだけで野矢論理に登場する各論理体系と対応するようになるのでお得です。お得なのでざっくり入門してみます。

PTSは (S,A,R)(\mathcal{S}, \mathcal{A}, \mathcal{R}) という3つ組で定義されます。

  • S\mathcal{S} ：ソートの集合
    • ソート：型や、より上位の階層を表す記号。例えば ∗* や □\square がある
    • ∗* ：真の型（通常の型。項を分類するもの）のあつまり
    • □\square ：カインド（型（真の型に限らない）を分類するもの）のあつまり
  • A⊂S2\mathcal{A} \subset \mathcal{S}^2 ：Axioms（公理）
    • ソートの2つ組の集合
    • ソート間の階層関係を決める
    • 今回扱う体系では {(∗,□)}\{(*, \square)\} 固定
  • R⊂S3\mathcal{R} \subset \mathcal{S}^3 ：Rules（規則）
    • ソートの3つ組の集合
    • どんな依存関係の関数（ラムダ抽象）が許されるかを決める
    • 今回扱う体系では2、3番目のソートは同じ

式 A,B⋯A, B \cdots は以下のように再帰的に定義されます。

  • A,B⋯:=A, B \cdots :=
    • ss （ソート）
      • S\mathcal{S} の要素
    • xx （変数）
    • λx:A. B\lambda x : A. ~ B （ラムダ抽象）
      • AA に属する変数 xx を受け取ると BB を返す関数
    • Πx:A. B\Pi x:A. ~ B （依存積）
      • ラムダ抽象が属する対象
      • AA はラムダ抽象の引数が属する対象。 BB はラムダ抽象の本体が属する対象
      • BB の内部で変数 xx を参照できるのが特徴
    • A BA ~ B （適用）
      • 関数 AA に BB を引数として渡す

型付け規則は7個あります。

ですが、今回は主にProd規則とAbs規則を使うので、他の規則は畳んでおきます。必要になったら参照していただければと思います。

Prod規則

Γ⊢A:s1Γ,x:A⊢B:s2Γ⊢Πx:A.B:s3((s1,s2,s3)∈R)\dfrac { \Gamma \vdash A : s_1 \quad \Gamma, x : A \vdash B : s_2 } { \Gamma \vdash \Pi x : A. B : s_3 } \quad ((s_1, s_2, s_3) \in \mathcal{R})

依存積の引数と本体がどうあるべきか、そして依存積自体が何に属するかを決めます。

s1s_1 は AA が属する対象、つまり「『引数 xx が属する対象』が属する対象」です。 s2s_2 は本体 BB が属する対象です。 s3s_3 は依存積自体が属する対象です。なお、今回扱う体系では s2=s3s_2 = s_3 なので、依存積が属する対象は、その本体が属する対象と同じになります。

したがって、Rulesにある s1s_1 と s2=s3s_2 = s_3 の組み合わせによって、 依存積の引数と本体にそれぞれ何を書いて良いかが決まります。

あと型付けを考える際のちょっとしたコツなのですが、ネストした依存積がある場合、最も外側の依存積が属する対象は、最も内側の本体が属する対象と同じになることに注意します。例えば、 nat:∗nat : * のとき (Πn:nat.(Πn:nat.nat)):∗(\Pi n : nat. (\Pi n : nat. nat)) : * です1

Abs規則

Γ,x:A⊢B:CΓ⊢(Πx:A.C):sΓ⊢(λx:A.B):(Πx:A.C)\dfrac { \Gamma, x : A \vdash B : C \quad \Gamma \vdash (\Pi x : A. C) : s } { \Gamma \vdash (\lambda x : A. B) : (\Pi x : A. C) }

ラムダ抽象が依存積に属することを規定します。

依存積なので、 CC はラムダ抽象に渡された引数 xx に依存できます。なので結論のラムダ抽象と依存積について、それらの引数と、引数が属する対象は同じになります。

最初の前提では、 xx が AA に属するとしたときに、ラムダ抽象の本体 BB が依存積の本体 CC に属することを要求しています。意味からして妥当ですね。

2つ目の前提では、依存積が何らかのソートに属することを要求しています。これによって、さきほどのProd規則が要求されて、正当なRulesに準拠した依存積であることがチェックされます。

他の規則

Ax規則

⊢s1:s2((s1,s2)∈A)\dfrac { } { \vdash s_1 : s_2 } \quad ((s_1, s_2) \in \mathcal{A})

ソートが属する対象をAxiomsで決定します。

今回扱う体系では ⊢∗:□\vdash * : \square だけです。

Var規則

Γ⊢A:sΓ,x:A⊢x:A(x∉dom(Γ))\dfrac { \Gamma \vdash A : s } { \Gamma, x : A \vdash x : A } \quad (x \notin dom(\Gamma))

変数が属する対象を決めます。

証明の際には規則を下からたどるので、結論部分は、 x:Ax : A を示したい状態のコンテキストに x:Ax : A が含まれることを要求しています。

前提では、 AA がどこかのソートに属することを要求しています。他の規則を見るとわかるのですが、例えばラムダ抽象はソートに属せないので、変数はラムダ抽象に属せないとわかります。

App規則

Γ⊢A:(Πx:B.C)Γ⊢D:BΓ⊢(A D):C[x:=D]\dfrac { \Gamma \vdash A : (\Pi x : B. C) \quad \Gamma \vdash D : B } { \Gamma \vdash (A ~ D) : C[x := D] }

適用の形式が属する対象を決めます。

1つ目の前提では、演算子 AA が依存積に属することを要求します。 AA はラムダ抽象でも、もっと複雑な式でも良いですが、最終的に依存積に属する必要があります。つまり、ソートとか型みたいな、呼び出せない（依存積に属さない）ものじゃないよね？というのをチェックしています。

2つ目の前提では、 BB を受け取る関数（ AA ）に DD を渡そうとしているけど、 DD は BB に属しているよね？というのを検査しています。例えばnumberを受け取る関数に123を渡す場合、123にnumber型が付くのをチェックするみたいな感じです。

最終的な結論では、適用が属する対象は、演算子 AA が属する依存積の本体について、 xx に DD を代入したものになります。適用したので、ラムダ抽象が1つはずれて本体が出てくる感じです。

Weak規則

Γ⊢A:BΓ⊢C:sΓ,x:C⊢A:B(x∉dom(Γ))\dfrac { \Gamma \vdash A : B \quad \Gamma \vdash C : s } { \Gamma, x : C \vdash A : B } \quad (x \notin dom(\Gamma))

Γ⊢A:B\Gamma \vdash A : B について、コンテキスト Γ\Gamma に余分な仮定を追加しても良いと言っています。

証明をするときには下から読むので、コンテキストから不要な変数を消すときに使います。コンテキストが空じゃないとAx規則が使えないですからね。

ただそれだけの規則なのですが、 CC はちゃんとソートに属していないとだめです。これはVar規則で見たのと同じやつです。

Conv規則

Γ⊢A:BΓ⊢B′:sΓ⊢A:B′(B=βB′)\dfrac { \Gamma \vdash A : B \quad \Gamma \vdash B' : s } { \Gamma \vdash A : B' } \quad (B =_{\beta} B')

Γ⊢A:B\Gamma \vdash A : B について、 BB の部分をベータ変換して B′B' になるなら置き換えても良いということです。

「 BB は型の場合があるけど、型を評価するって何？」と思われるかもしれません。依存型がある体系では、型の中に評価可能な式が含まれる場合があります。なので、2つの型の同一性を判定するには、型検査の途中でこのような評価が必要です。詳しくは「自作してふんわり眺める依存型【定理証明】」を参照ください。

Rocqで実装してみた

私はかなりポンコツなので、式変形や規則の適用を99割くらいミスります。なので、Rocq上にPTSを定義して、証明とかを書けるようにしました。

記事中のいくつかの型付けはこれでチェックしています。

正直、ここまでの定義はかなりざっくりしているので、詳細はRocqのコードか参考文献を参照ください。

命題論理

前置きが非常に長くなってしまいましたが、いよいよ論理学に入門していきます。

以下のようにすると、単純型付きラムダ計算になって、これは命題論理に対応します2

S={∗,□}A={(∗,□)}R={(∗,∗,∗)}\begin{aligned} \mathcal{S} &= \{*, \square\} \\ \mathcal{A} &= \{(*, \square)\} \\ \mathcal{R} &= \{(*, *, *)\} \\ \end{aligned}

(∗,∗,∗)(*, *, *) は、項に依存する項を許します。

プログラミングの視点

項に依存する項というのは、普通の関数のことです。

自然数型 nat:∗nat : * があるとします。Prod規則より Πn:nat.nat\Pi n : nat. nat という型が許されます3

Γ⊢nat:∗Γ,n:nat⊢nat:∗Γ⊢Πn:nat.nat:∗((∗,∗,∗)∈R)\dfrac { \Gamma \vdash nat : * \quad \Gamma, n : nat \vdash nat : * } { \Gamma \vdash \Pi n : nat. nat : * } \quad ((*, *, *) \in \mathcal{R})

なので、それに属する λn:nat.n\lambda n : nat. n という項も書けます4

Γ,n:nat⊢n:natΓ⊢(Πn:nat.nat):∗Γ⊢(λn:nat.n):(Πn:nat.nat)\dfrac { \Gamma, n : nat \vdash n : nat \quad \Gamma \vdash (\Pi n : nat. nat) : * } { \Gamma \vdash (\lambda n : nat. n) : (\Pi n : nat. nat) }

これは自然数を受け取ってそのまま返すという、普通のid関数ですね。

論理の視点

なにか適当な型 A:∗A : * があるとします。

さきほどと同様に、 Πx:A.A\Pi x : A. A という型と、 λx:A.x\lambda x : A. x という項が書けます。

ここで、カリー＝ハワード同型対応により、「型＝命題」であり「プログラム＝証明」と考えてみます。すると、野矢論理の第1章第1節付近で言われていることは以下のように対応します。

  • AA ：命題記号。原子式とも
  • 型「 Πx:A.A\Pi x : A. A 」：命題「AならばA」
  • ↑の型に属する項「 λx:A.x\lambda x : A. x 」：↑の命題の証明
  • 項の簡約：証明の簡約

また、野矢論理第3章第4節で言われているメタ論理周辺の用語については、以下のように考えられます。

  • 健全性
    • プログラミング：型が付けば、実行時におかしくならない
    • 論理：構文論で導出された定理は、意味論での論理的真理である
  • 完全性
    • プログラミング：実行時におかしくならないなら、型が付く
    • 論理：意味論で論理的真理ならば、構文論でも導出できる

述語論理

単純型付きラムダ計算のルールに (∗,□,□)(*, \square, \square) を追加します。これによってLogical Framework（LF）と呼ばれる型システムができて、これは述語論理に対応します。

S={∗,□}A={(∗,□)}R={(∗,∗,∗),(∗,□,□)}\begin{aligned} \mathcal{S} &= \{*, \square\} \\ \mathcal{A} &= \{(*, \square)\} \\ \mathcal{R} &= \{(*, *, *), (*, \square, \square)\} \\ \end{aligned}

追加された (∗,□,□)(*, \square, \square) は、項に依存する型を許します。

プログラミングの視点

(∗,□,□)(*, \square, \square) 規則によって、 Πn:nat.∗\Pi n : nat. * といった依存積が許されます5

Γ⊢nat:∗Γ,n:nat⊢∗:□Γ⊢Πn:nat.∗:□((∗,□,□)∈R)\dfrac { \Gamma \vdash nat : * \quad \Gamma, n : nat \vdash * : \square } { \Gamma \vdash \Pi n : nat. * : \square } \quad ((*, \square, \square) \in \mathcal{R})

ここで、「自然数nを受け取って、nが偶数であるという命題を返す関数」を eveneven と書くことにします。

eveneven はさきほどの依存積に属します。まず eveneven の引数部分は、自然数nを受け取るので λn:nat.⋯\lambda n : nat. \cdots となります。依存積の引数部分と同じですね。次に本体部分がどうなるかですが、その体系で自然数や偶数が具体的にどう構成されるのかによります。しかし、少なくとも「nが偶数であるという命題」、つまり型を返すので、 even:(Πn:nat.∗)even : (\Pi n : nat. *) となります。

論理の視点

野矢論理の第2章第2節に登場する述語論理の用語は、以下のように対応すると考えられます。

  • （個体）変項：個体を値域に持つ変数。 xx 、 yy 、 zz のように表される
    • プログラミングでは： n:natn : nat の nn のような変数
  • （個体）定項：変項の値となる固有名。 aa 、 bb 、 cc のように表される
    • プログラミングでは： 11 、22 、33 など
  • 命題：真偽を問題にできる文。 FaFa などと表される
    • プログラミングでは： ∗* に属するもの。例えば even 2even ~ 2 は ∗* に属する6ので命題。したがって ∗* は命題の集まり（宇宙）と考えられる
  • 命題関数：命題の「個体を表す部分」を「変項」に置き換えた文。個体から命題への関数。 FxFx などと表される
    • プログラミングでは：項から型への関数。 eveneven など
  • 述語：個体が満たす性質や関係を表した表現。命題関数の変項以外の部分。 FF 、 GG などで表される
    • プログラミングでは： eveneven の変数以外の部分など
  • 全称量化：命題関数の変項に「すべて」という量を与えること。例えば「すべての自然数nは偶数である」
    • プログラミングでは：依存積。例えば上記の命題は、 Πn:nat.even n\Pi n : nat. even ~ n に対応する。なお、このように本体で引数を使っている依存積は、依存型と呼ばれる。
  • 自由変項：量化されていない変項。「nは偶数である」（ even neven ~ n ）の nn は自由変項
  • 束縛変項：量化されている変項。「すべての自然数nは偶数である」（ Πn:nat.even n\Pi n : nat. even ~ n ）の nn は束縛変項。
  • 束縛変項は実質的に変項ではない
    • 「すべての自然数nは偶数である」の nn に2を代入して「すべての自然数2は偶数である」のようにはできない。意味が変わってしまうため。
    • nn は量化によっていわば代入済みになっている。実際、 Πn:nat.even n\Pi n : nat. even ~ n は ∗* に属する7ため、これは命題関数ではなく命題になっている。
  • 議論領域：議論されている範囲。今回の例では自然数（ natnat ）のこと。

三段論法

野矢論理によれば、三段論法は伝統的論理学（アリストテレスから始まり、フレーゲが述語論理を構築するまで支配的だった論理学）のものらしいです。そしてアリストテレスは、三段論法を（論法の格や、各文の型によって）256種類に分類し、そのうち24種類が正しいことを公理的方法で証明したそうです。

これが、冒頭の「三段論法はどうして成り立つのか？」に対する答えで、ちゃんと本に書いてありました。

それどころか、正しい三段論法は述語論理でも証明できる8ことまで書かれていました。

例えば、議論領域をdomain、Hxを「xは人間である」、Mxを「xは死ぬ」とおきます。つまり以下のようなコンテキストがあるとします。

  • domain:∗domain : *
  • H:(Πx:domain.∗)H : (\Pi x : domain. *)
  • M:(Πx:domain.∗)M : (\Pi x : domain. *)
  • socrates:domainsocrates : domain

そして「すべての人間は死ぬ、ソクラテスは人間である、ゆえにソクラテスは死ぬ」という命題は、以下のようにLF上の式として表せます。

ΠHxMx:(Πx:domain.(ΠHx:(H x).M x)).(ΠHsocrates:(H socrates).M socrates)\Pi HxMx : (\Pi x : domain . (\Pi Hx : (H ~ x) . M ~ x ) ) . (\Pi Hsocrates : (H ~ socrates) . M ~ socrates )

（なお、HxMx、Hx、Hsocratesなど、変数名がフリーダムになっています。わかりやすさのためにこのように表記しましたが、読みづらかったらすみません）

数式だけだと見づらいかもなので、元のコードも貼っておきます。HxMxは、「xは人間である」を受け取って「xは死ぬ」を返す関数です。Hsocratesは、ソクラテスが人間である証拠です。

\Pi
  HxMx :
    (\Pi
      x :
        domain
      .
        (\Pi
          Hx :
            (H ~ x)
          .
            M ~ x
        )
    )
  .
    (\Pi
      Hsocrates :
        (H ~ socrates)
      .
        M ~ socrates
    )

これに属する式を考えて、LFによる型付けが導出できたなら、その三段論法は正しいということになります。そして実際、Rocq上で導出の証明が通った9のでこの論法は正しいとわかりました。

二階述語論理

せっかくPTSを導入したので、もうちょっと先の体系まで見てみたいと思います。ただ、冒頭の三段論法の疑問自体は解消しているので、かなり概観だけ眺めます。

LFに (□,∗,∗)(\square, *, *) 規則を追加すると λP2\lambda P2 となって、二階述語論理に対応します。

S={∗,□}A={(∗,□)}R={(∗,∗,∗),(∗,□,□),(□,∗,∗)}\begin{aligned} \mathcal{S} &= \{*, \square\} \\ \mathcal{A} &= \{(*, \square)\} \\ \mathcal{R} &= \{(*, *, *), (*, \square, \square), (\square, *, *)\} \\ \end{aligned}

追加された (□,∗,∗)(\square, *, *) は、型に依存する項を許します。

プログラミングの視点

型に依存する項というのは、プログラミングではジェネリクスやパラメータ多相に相当します。

例えば以下のTypeScriptのコードでは、任意の型Aを受け取って、Aのid関数を返しています。

const id = <A>(a: A): A => a;

論理の視点

命題受け取って証明を作れるという感じです。

例えば、命題Aを受け取って「AならばA」の証明を作る関数は、 λA:∗.λx:A.x\lambda A : *. \lambda x : A. x となって、 これは ΠA:∗.Πx:A.A\Pi A : *. \Pi x : A. A に属し、 (□,∗,∗)(\square, *, *) 規則によって許されます10

「命題Aを受け取って」のように、変項（A）に個体ではなく命題を取れるのが二階述語論理の特徴です。

野矢論理第3章付論では、「トキが2羽いる」という文を扱っています。「〜〜が2羽いる」という述語について、〜〜の部分に個体（具体的なトキの名前）ではなく、述語（トキ）が入ることを説明しています。

つまり。「2」というのは個体に対する述語ではなく、述語に対する述語であるということでした。したがって、「数」というものを述語論理に取り込もうとしたフレーゲが、自然と二階の述語論理に踏み出してしまい、それがラッセルのパラドックスにつながっていったということらしいです。

高階述語論理

二階述語論理に (□,□,□)(\square, \square, \square) 規則を追加するとCalculus of Constructions（CC）となって、高階述語論理に対応します。

S={∗,□}A={(∗,□)}R={(∗,∗,∗),(∗,□,□),(□,∗,∗),(□,□,□)}\begin{aligned} \mathcal{S} &= \{*, \square\} \\ \mathcal{A} &= \{(*, \square)\} \\ \mathcal{R} &= \{(*, *, *), (*, \square, \square), (\square, *, *), (\square, \square, \square)\} \\ \end{aligned}

追加された (□,□,□)(\square, \square, \square) は、型に依存する型を許します。

プログラミングの視点

型に依存する型というのは、型演算子、型コンストラクタに対応します。

例えば以下のTypeScriptのコードでは、任意の型Aを受け取って、「Aを受け取ってAを返す関数型」を返しています。

type Id<A> = (a: A) => A;

論理の視点

命題を受け取って命題を作れるという感じです。

例えば、命題Aを受け取って「AならばA」という命題を返す関数は、 λA:∗.Πx:A.A\lambda A : *. \Pi x : A. A となって、これは ΠA:∗.∗\Pi A: *. * に属するので、 (□,□,□)(\square, \square, \square) によって許されます11

二階述語論理の例と違って、返しているのが証明ではなく命題であることに注意します。

ラムダキューブ

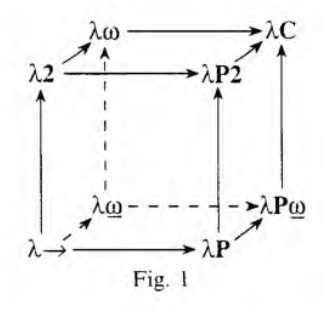
ここまで見てきた体系は、ラムダキューブの各頂点として整理されます。

ラムダキューブ

出典: Pierce, Benjamin C. 型システム入門 プログラミング言語と型の理論. 株式会社 オーム社, 2013.、第30章、p.368

左下の λ→\lambda_{\rightarrow} が単純型付きラムダ計算で、 (∗,∗,∗)(*, *, *) の規則だけを持ちます。ここに、

  • (∗,□,□)(*, \square, \square) 規則を追加すると右に行ける
  • (□,∗,∗)(\square, *, *) 規則を追加すると上に行ける
  • (□,□,□)(\square, \square, \square) 規則を追加すると奥に行ける

という感じです。すべての規則を入れると、キューブの中で最強の体系であるCalculus of Constructions（CC）に到達します。

こいつにソートの階層構造やら帰納型やらを入れると、Calculus of Inductive Constructions（CIC）になって、Rocqのコアの型システムになるそうです。

ラムダキューブの外

PTSを使うと、キューブの外にある体系も表せます。

例えば、System U−\text{U}^- は以下のように定義できます。

S={∗,□,△}A={(∗,□),(□,△)}R={(∗,∗,∗),(□,∗,∗),(□,□,□),(△,□,□)}\begin{aligned} \mathcal{S} &= \{*, \square, \triangle\} \\ \mathcal{A} &= \{(*, \square), (\square, \triangle)\} \\ \mathcal{R} &= \{(*, *, *), (\square, *, *), (\square, \square, \square), (\triangle, \square, \square)\} \\ \end{aligned}

これは、前回の「自作の定理証明系を弱めてパラドックスを回避しよう」で、ハーケンスのパラドックスが構成された体系です。

ハーケンスの論文を読んだ際、前回の記事では、

宇宙語すぎて「へへ……」みたいな謎の笑いしか出ませんでした。

とか、

□とか△とかが楽しそうにしてるねぇ

みたいなことしかわかりませんでした。

まぁ数学的なバックグラウンドが無いので、パラドックスが構成される理由や背景を理解するのは現状でも無理です。しかし、少なくとも宇宙語という感じは無くなって、書いてある意味くらいは分かるなぁとなってきました。

PTSのおかげですね。

所感

本が良かった

『論理学』 野矢茂樹（東京大学出版会）は良かったです。冒頭の三段論法の疑問もキッパリ解消してくれましたし、単に定義を並べるだけの難しい本ではなく、一部が会話形式になっているのが面白いと感じました。野矢先生（教える側）と、無門と道元（教わる側）の3人が登場して、例えば以下のような会話をしています。

条件法の定義

  • 野矢：（略）条件法の真理関数の定義から考えてみましょうか。
  • 無門：前件が偽のときがどうもしっくりこないんじゃ。
  • 野矢：でしょうね。
  • （略。日常における条件法の例を会話の中で検討して、やはり疑問が残る）
  • 野矢：（略）いまわれわれにとっての課題は、こうした日常言語の「ならば」のある側面をもっともよく捉えているような真理関数をどう定義すればよいか、という問題なんです。

出典：『論理学』 野矢茂樹（東京大学出版会）、第1章、第1節、p.29、略と要約は筆者による

無門と道元が「わからない」と言ってくれるので、「ここはつまづきやすいポイントなんだな」と認識できますし、難しい定義が出てきたら「なんで？」と野矢先生に質問してくれるので、納得感を持って進んでいけるのが良かったです。SS速報VIPを読んで育った世代なので、こういう形式には適正があります。

一方で、公理系や証明などのカッチリしたやつも程よく散りばめられていて面白かったです。会話中、『論理哲学論考』（ウィトゲンシュタイン）について、無門と道元という初心者相手に「ええ、読むことをお勧めします」と言ってしまうあたりは、ちょっと狂気を隠しきれていない感じで好きでした。

あまり関係ないんですけど、論理哲学論考ってコミックシーモアで立ち読みできるらしいです。そうなの？

PTSがお得だった

今回、はじめて純粋型システムを触ってみたのですが、いままで別々の体系として考えていたものが統一的に理解できてとても良かったです。

あるHaskellコミュニティで、PTSについて説明している人の動画をみたのですが、

Haskellには恐ろしい拡張機能（のオプション）がたくさんあります。威圧的です。

  • -XTypeFamilies
  • -XExistentialQuantification
  • -XRank2Types
  • -XRankNTypes
  • -XDataKinds
  • -XPolyKinds
  • -XGADTs
  • -XConstraintKinds
  • -XImpredicativeTypes
  • etc...

PTSは、これらの-Xfoobarを1つのフレームワークで理解する方法です。

つまり、たくさんのクレイジーなものを理解する代わりに、1つのクレイジーなものを理解するだけで済みます。

出典：Cody Roux - Pure Type Systems - YouTube、意訳は筆者による

よくわかります。

実際今回も、PTSのパラメタを変えるだけでラムダキューブに属するすべての体系を作りだせることがわかりましたし、おまけでハーケンスの論文も宇宙語じゃなくなりました。とてもお得です。

まとめ

論理学と型システムへ同時に入門してみました。冒頭の「論理学って結局なに？」を解決するために、プログラミングに対応させて理解してみました。

論理学の定義は抽象的になりがちなので、たまに何について考えているのかわからなくなります。そういうときは、プログラミングの世界で考え直し、またRocqで具体的に構成することで、「あ〜コードでいうところのアレね？」みたいに実感しやすくなりました。

抽象を抽象のまま理解できたら効率が良いと思うのですが、それができないあたりは、自分はプログラマー向きなんだなと思うところです。

論理学と型システムの両方の初心者なので、おかしなことを書いているかもしれません。また、両者の対応についてはもっと怪しくて、自分なりに考えて裏取りもしているのですが、正直自信がありません。

なので、ツッコミどころがあればマサカリを投げていただけると嬉しいです。

ありがとうございました。

参考文献

  1. (Πn:nat.(Πn:nat.nat)):∗(\Pi n : nat. (\Pi n : nat. nat)) : * の証明↩
  2. より正確には、直観命題論理（古典命題論理の二重否定除去を爆発律に弱めたやつ）に対応します。↩
  3. Πn:nat.nat:∗\Pi n : nat. nat : * の証明↩
  4. (λn:nat.n):(Πn:nat.nat)(\lambda n : nat. n) : (\Pi n : nat. nat) の証明↩
  5. (Πn:nat.∗):□(\Pi n : nat. *) : \square の証明↩
  6. (even 2):∗(even ~ 2) : * の証明↩
  7. (Πn:nat.even n):∗(\Pi n : nat. even ~ n) : * の証明↩
  8. 厳密には古典述語論理では可能ということで、それより弱い直観主義述語論理でも可能かは確認の余地があるかもしれません。ただ少なくとも、直観主義述語論理側で証明が通ったなら、その論法は正しいとは言えそうです。↩
  9. 「すべての人間は死ぬ、ソクラテスは人間である、ゆえにソクラテスは死ぬ」の証明↩
  10. (λA:∗.λx:A.x):(ΠA:∗.Πx:A.A)(\lambda A : *. \lambda x : A. x) : (\Pi A : *. \Pi x : A. A) の証明↩
  11. (λA:∗.Πx:A.A):(ΠA:∗.∗)(\lambda A : *. \Pi x : A. A) : (\Pi A: *. *) の証明↩

続けて読む…

SICPの備忘録

2023/07/29

ざっくりホーア論理

2024/09/28

よわよわエンジニアがTAPL（型システム入門）を読んだら

2022/05/02

TypeScriptの型で全加算器から浮動小数点数，そして√2

2021/06/07

ほぼ関数だけでFizzBuzzしてツイートしたい【JavaScript】

2025/03/24

TypeScriptの型で素数を求めたい

2021/01/19

書いた人

sititou70のアイコン画像
sititou70

都内の社会人エンジニア5年生。Web技術、3DCG、映像制作が好き。