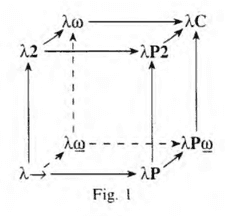
自作してふんわり眺める依存型【定理証明】

ぼく「Geminiさん、依存型を実装して詳しく理解したいのですが良い資料ありませんか？」

Gemini「A tutorial implementation of a dependently typed lambda calculusっていう論文がおすすめです」

というわけで

依存型について理解するために、A tutorial implementation of a dependently typed lambda calculusを読みました。

この記事は、理論編と実装編に分かれています。

理論編では、上記の論文で示されている構文、型付け規則、評価規則をざっくりと紹介しようと思います。できるだけ難しい用語は使わず、自分のための補足説明も入れていこうと思います。

実装編では、本論文のコードをTypeScriptへ写経します。

リポジトリ：https://github.com/sititou70/lambda-pi

そして、より実践的な例として、すべての自然数 $n$ について

が成り立つことの証明を構築します。

理論編

抽象構文

抽象構文とは、主に理論編の中で使用する構文です。プログラムや型をテキストで表して議論するために使用します。

$e$ を任意の項（プログラム）、 $\rho$ （ロー）を任意の型、 $\kappa$ （カッパ）を任意のカインド（型の型）とします。

ここでさっそく驚きポイントなのですが、今回の体系ではこれら3つを構文上で区別しません。これにより型の中に項が書けるようになって、項に依存した型で依存型というわけです。前回の記事で、「依存型の中では型とプログラムのどっちを書いているのか混乱する」と言っていたやつですね。

前置きが長くなりましたが、今回の抽象構文は以下のようになります。

• $e, \rho, \kappa ::=$
  • $e :: \rho$ （注釈された項）
    • $e$ が $\rho$ 型であるという主張です。
    • TypeScriptの型注釈に似ています。
  • $*$ （型の型）
    • 型の型を表します。
    • 型（命題）を受け取る関数を型付けしたいときに使う感じです。これにより、「すべての命題について〜」というような命題が定義できます。詳しくは前回の記事の、カリーハワード同型対応の説明を参照ください。
  • $\forall x :: \rho. \rho'$ （依存関数型）
    • 関数型（アロー型）の依存型バージョンです。
    • 「$\rho$ の変数 $x$ を受け取って、 $\rho'$ 型の項を返す関数の型」という意味です。
    • 命題を表す際によく使います。例えば、 $\forall x :: \text{Nat}. \rho'$ と書くと、「自然数 $x$ について、 $\rho'$ （ $x$ を使った等式の型などが書ける）が成り立つ」という意味になります。
  • $x$ （変数）
  • $e ~ e'$ （適用）
    • e(e')の意味です。
  • $\lambda x \rightarrow e$ （ラムダ抽象）
    • 関数のことです。 $x$ が引数で $e$ が関数本体です。
    • $\forall x :: \rho. \rho'$ 型が付く項です。
    • 今回の構文では $x$ の型を明示しません。後述する型付け規則を見るとわかるのですが、注釈によって対応する $\forall x :: \rho. \rho'$ の $\rho$ からわかるので不要みたいです。
  • $\text{Nat}$ （自然数型）
  • $\text{Zero}$ （自然数のゼロのコンストラクタ）
  • $\text{Succ} ~ e$ （自然数の後者のコンストラクタ）
    • $e$ の次の数を表します。
  • $\text{natElim} ~ e_1 ~ e_2 ~ e_3 ~ e_4$ （自然数の除去）
    • 自然数に関する示したい命題（ $e_1$ ）について、Zeroのケース（ $e_2$ ）と、Succのケース（ $e_3$ ）で成り立つことが言えるなら、任意の自然数（ $e_4$ ）で命題が成り立つと言っていいよという意味です。
      • $e_1$ ：自然数を受け取って型（命題）を返す関数です。最終的に示したい命題です。
      • $e_2$ ：$e_1 ~ Zero$ 型の項です。つまり、$e_1$ がゼロで成り立つ証明です。
      • $e_3$ ：自然数 $n$ と、 $e_1 ~ n$ 型の項を受け取ると、$e_1 ~ \text{Succ} ~ n$ 型の項を返す関数です。つまり、示したい命題がある自然数で成り立つことを仮定して、次の自然数でも成り立つことを示す証明です。
      • $e_4$ ：natElimを適用する自然数です。自然数であれば何でも良いです。
      • 最終的に、この項には $e_1 ~ e_4$ 型が付きます。 $e_4$ は自然数であれば何でも良かったので、すべての自然数に対して $e_1$ が成り立つ気持ちです。
    • 高校の数学の授業でやった、数学的帰納法に似てますね。
    • ElimはEliminatorの略だそうで、Rocq（旧Coq）のelimタクティックと語源が一緒っぽいです。このへんあまり詳しくないのですが、最終的に自然数 $e_4$ が消えるので、除去規則的な意味でEliminatorと言ってるんすかね？
  • $\text{Eq}$ （Eq型）
  • $\text{Refl} ~ e$ （Eqのコンストラクタ）
    • $e = e$ の意味です。
    • これはRocqでのEqの定義に似ています。
  • $\text{eqElim} ~ e_1 ~ e_2 ~ e_3 ~ e_4 ~ e_5 ~ e_6$ （Eqの除去）
    • ある型（ $e_1$ ）があって、その型の等式に関する示したい命題（ $e_2$ ）について、Reflのケースで命題が成り立って（ $e_3$ ）、ある左辺の値（ $e_4$ ）と右辺の値（ $e_5$ ）があって、それらが実際に等しい（ $e_6$ ）ならば命題が成り立つという意味です。
      • $e_1$ ：両辺の値の型です。今回の証明では主に $\text{Nat}$ です。
      • $e_2$ ：最終的に示したい命題で、左辺の値、右辺の値、左辺と右辺が等しいというEq型の値を受け取って、命題を返す関数です。
      • $e_3$ ：$e_1$ 型の値 $z$ を受け取ると、 $e_2 ~ z ~ z ~ (\text{Refl} ~ e_1 ~ z)$ 型の値を返す関数です。これはReflコンストラクタに対応したケースですね。
      • $e_4$ ：$e_1$ 型の左辺の値です。
      • $e_5$ ：$e_1$ 型の右辺の値です。
      • $e_6$ ：$\text{Eq} ~ e_1 ~ e_4 ~ e_5$ 型の値です。 $e_4$ と $e_5$ が本当に等しいのか示してみろということです。
      • 最終的に、この項には $e_2 ~ e_4 ~ e_5 ~ e_6$ 型が付きます。等しいすべての $e_4$ と $e_5$ について、 $e_2$ が成り立つというわけです。
    • RocqでのEqの帰納的な定義を思い出して、Eqに対する帰納法の原理と考えるとわかりやすいかもです。

型付け規則

型付け規則は、さきほどの構文にどのような型が付くのかを定義します。

さっそく、$e :: \rho$ （注釈された項）の型付け規則であるT-Annを見てみましょう。

この分数のような記法は「線の上（仮定）のすべての式が成り立つならば、線の下（結論）の式が成り立つ」という意味です。

$\Gamma \vdash e ::_\uparrow \rho$ や $\Gamma \vdash e ::_\downarrow \rho$ は、型付け判別式で、「コンテキスト $\Gamma$ のもとで、 $e$ に $\rho$ 型が付く」という意味です。

$\Gamma$ はコンテキストで、変数と型のマッピングを保持しています。TypeScript風に書くとMap<variable, type>みたいなやつです。今回の規則ではただあるだけという感じですが、他の規則ではコンテキスト内のマッピングを取得（Map.prototype.get()）したり、コンテキストに新しいマッピングを追加（Map.prototype.set()）したりもします。簡単のために詳しい定義は割愛します。

$::_\uparrow$ は型推論モードを、 $::_\downarrow$ は型検査モードを意味します。これは双方向型検査と呼ばれる仕組みのようで、今回のような強い型システムで型推論する手法の1つだそうです。正直むずかしいので、最初はこの上下の矢印を無視して読むくらいが良いかもしれません。詳しくはMizunashi Manaさんの「双方向型検査: 検査と構築の融合」が参考になります

$e \Downarrow e'$ は、 $e$ を評価すると最終的に $e'$ になるという意味です。ここで驚きポイントその2なのですが、今回の計算体系では、型検査の際に評価（プログラムの実行）が発生する場合があります（！）

以上を踏まえて、もう一度T-Annを見てみましょう。

まず結論をみると上矢印があるので、注釈された項は推論モードで扱える（項だけから型がわかる）と言っています。実際、 $e$ の型が $\rho$ と明示されているのでそれはそうだよなという感じです。

推論の具体的なステップは、仮定部分を見るとわかります。まず仮定の最初の式では、 $\rho$ が $*$ 型であることを検査していますね。これにより、注釈の型の部分に項が書かれているような不正なケースを弾いています。

それがOKなら仮定の次の式によって、 $\rho$ を評価して、最終的な評価結果である $\tau$ を得ます。ここで私は最初「型を評価するってなに？」となったので、つまづきポイントだと思います。

今回の体系では項と型を区別していないので、型に対する評価規則も定義されます（後の評価規則の節で説明します）。なので、 $\rho$ も評価すると別の形になるかもしれません。具体的には、型が項に依存しているかもしれず（依存型）、型の中に評価すると形が変わる項があるかもしれません。なので、型付け規則全体を通して、型は評価したうえで検査に使用する方針に統一されているようです。これにより、「評価すると実質的に同じになる型」を同一視できるようになります。

実際、仮定の最後の式では、 $e$ が $\tau$ 型である（つまり注釈が正しい）ことを、評価後の型を使って検査していますよね。

評価規則

今回の最終的な目標は定理の証明なので、型（命題）とプログラム（証明）が合っているかを型検査できれば良いです。なので型付け規則だけ考えれば良い、と思っていた時期が僕にもありました。

この体系では型検査の途中に評価もするので、評価規則もまじめに勉強しないとダメでした。

というわけで、評価規則を1つ見てみましょう。E-Ann規則は以下のようになっています。

注釈された項の後の部分が $v$ に評価されるなら、もとの注釈された後全体も $v$ に評価して良い、と言っています。

つまり、注釈された型情報を捨てて評価しているという感じです。TypeScriptっぽいですね。

現時点で記事がかなり長くなっている自覚があります。なので、のこりの規則は畳んでおきます。

実装編

理論編の内容をTypeScriptに実装しました。論文ではHaskellによる実装が示されているので、それを写経した感じです。

リポジトリ：https://github.com/sititou70/lambda-pi

まず、配列を使って項を表すことにしました。パーサーとかを考えたくなかったからです。

抽象構文をもとに、以下のような具象構文を定義します。

export type TermInferable =
  | ["Ann", TermCheckable, TermCheckable]
  | ["Star"]
  | ["Pi", TermCheckable, TermCheckable]
  | ["Bound", number]
  | ["Free", Name]
  | [TermInferable, ":@:", TermCheckable]
  | ["Nat"]
  | ["NatElim", TermCheckable, TermCheckable, TermCheckable, TermCheckable]
  | ["Zero"]
  | ["Succ", TermCheckable]
  | ["Eq", TermCheckable, TermCheckable, TermCheckable]
  | ["Refl", TermCheckable, TermCheckable]
  | [
      "EqElim",
      TermCheckable,
      TermCheckable,
      TermCheckable,
      TermCheckable,
      TermCheckable,
      TermCheckable
    ];

export type TermCheckable = ["Inf", TermInferable] | ["Lam", TermCheckable];

項には、推論可能な項（推論モードで扱える項）と検査可能な項（検査モードで扱える項）があり、構文レベルで区別されています。

次に、これらの項を検査するための関数を用意します。

export const typeInferable =
  (index: number) =>
  (context: Context) =>
  (term: TermInferable): Type => {
    // ...
  };

export const typeCheckable =
  (index: number) =>
  (context: Context) =>
  (term: TermCheckable) =>
  (type: Type): void => {
    // ...
  };

推論モードと検査モードの2種類の関数があります。推論モードの関数では、項を受け取って推論結果の型を返しています。一方で検査モードの関数では、項と型を受け取って、項にその型が付くか検査して、最終的には何も返しません。検査に成功するとそのまま終了して、失敗すると例外を投げます。indexとかContextとかTypeの説明は省略します。詳しい解説は論文を参照ください。

次に、評価のための関数も用意します。

export const evalInferable =
  (term: TermInferable) =>
  (env: Env): Value => {
    // ...
  };

export const evalCheckable =
  (term: TermCheckable) =>
  (env: Env): Value => {
    // ...
  };

推論可能な項のための関数と、検査可能な項のための関数を2種類作りました。ただ、評価には推論モードや検査モードという考えはないです。単純に型検査器と実装を対応させて見やすくするためにこうしました。

どちらの関数も、項を受け取って評価結果の値を返しています。例によって、EnvやValueの説明は省略します。

関数内部の具体的な実装は、基本的には理論編の規則をそのまま対応させればOKです。

例えば、T-Annを実装したいとします。これは推論モードの規則なので、typeInferable関数の中に次のように書けば良いです。

if (term[0] === "Ann") {
  const [_, exp, type] = term;
  typeCheckable(index)(context)(type)(["VStar"]);
  const evaluetedType = evalCheckable(type)([]);
  typeCheckable(index)(context)(exp)(evaluetedType);
  return evaluetedType;
}

注釈の項と型について、型がカインド型であることを検査し、それを評価したうえで、項にその型が付くことを検査しています。

T-Annと見比べると、同じことをやっているとわかります。

ただ、Haskellの型検査の実装と、論文中の型付け規則が違っている箇所がいくつかありました。例えば、Haskellの方では評価された項を使っているが、規則の方には評価するとは特に書かれていないということがありました。この場合は、基本的にはHaskellの方を優先していますが、まぁケースバイケースの雰囲気でなんとかしました。

かんたんな証明を書いてみよう

実装ができたのでさっそく証明を書いていきましょう。

まず、足し算x + yを以下のように定義します。

const plus: TermCheckable = [
  "Lam", // arg: x
  [
    "Inf",
    [
      "NatElim",
      // NatElim_prop
      // 自然数xについて、自然数yを受け取るとx + yを返す関数があるという命題です。
      [
        "Lam", // arg: x
        [
          "Inf",
          [
            "Pi",
            // 自然数yを受け取ると
            ["Inf", ["Nat"]],
            // 自然数x + yを返す
            ["Inf", ["Nat"]],
          ],
        ],
      ],
      // NatElim_propZero
      // xがゼロのときは、yが与えられたらそれをそのまま返す関数（恒等関数）が足し算の実装になります。
      // ["Inf", ["Bound", 0]]は直前のLamで受け取った引数を表します。0はド・ブラウン・インデックスです。つまり、一番内側で束縛された変数を参照しています。
      [
        "Lam", // arg: y
        ["Inf", ["Bound", 0]], // y
      ],
      // NatElim_propSucc
      // xがSuccの形で書ける、つまりxの前者x'がある場合です。
      // x'と、prop x'（つまり、足し算をx'に適用した項）を受け取って、足し算の実装を返せば良いです。
      [
        "Lam", // arg: x'
        [
          "Lam", // arg: prop x'
          [
            // 足し算の実装。yを受け取ってx + yを返します。
            // まず、「x' +」の意味のprop x'があるので、それをyに適用して「x' + y」を作ります。
            // あとはそれをSuccすれば、「Succ (x' + y)」、つまり「Succ(x') + y」ということで結局「x + y」が計算できたことになります。
            "Lam", // arg: y
            [
              "Inf",
              [
                "Succ",
                [
                  "Inf",
                  [
                    ["Bound", 1], // prop x'
                    ":@:",
                    ["Inf", ["Bound", 0]], // y
                  ],
                ],
              ],
            ],
          ],
        ],
      ],
      // NatElim_nat
      // NatElimをxに適用します
      ["Inf", ["Bound", 0]], // x
    ],
  ],
];
const plusType: TermCheckable = [
  "Inf",
  [
    "Pi",
    // 自然数xを受け取って
    ["Inf", ["Nat"]],
    [
      "Inf",
      [
        "Pi",
        // 自然数yを受け取ったら
        ["Inf", ["Nat"]],
        // x + yの自然数を返します
        ["Inf", ["Nat"]],
      ],
    ],
  ],
];
export const plusAnn: TermInferable = ["Ann", plus, plusType];

手始めに「すべての自然数nについて、 $0 + n = n$ 」の命題と証明を構築してみましょう。

まず、命題を型で表現します。

// 「自然数nを受け取って、0 + n = n型を返す関数」の型
const plusZeroLType: TermCheckable = [
  "Inf",
  [
    "Pi",
    // 自然数nを受け取って
    ["Inf", ["Nat"]],
    // 以下の型を返します
    [
      "Inf",
      [
        "Eq",
        // 自然数に関する等式があって、
        ["Inf", ["Nat"]],
        // 左辺は0 + n
        [
          "Inf",
          [
            [
              // さっき作った足し算を使います
              plusAnn,
              ":@:",
              ["Inf", ["Zero"]], // 0
            ],
            ":@:",
            ["Inf", ["Bound", 0]], // n
          ],
        ],
        // 右辺はn
        ["Inf", ["Bound", 0]], // n
      ],
    ],
  ],
];

この型が付く関数があれば、目的の命題が示されたことになります。そのような関数は、実は以下のように簡単に書けます。

// nを受け取って、Refl Nat nを返します。
// Rocqがわかる人向けだと、intro n. reflexivity.しただけです。
const plusZeroLProof: TermCheckable = [
  "Lam", // arg: n
  ["Refl", ["Inf", ["Nat"]], ["Inf", ["Bound", 0]]],
];

というのも、命題の型の左辺が評価されて簡単になるからです。

1. まずplusAnnを0に適用していますが、plusAnnの定義より恒等関数に評価されます。
2. 次に恒等関数をnに適用しています。当然、評価結果はnです。

で、右辺もnなので、その値はRefl Nat nで良いということです。

このことを型検査で確かめてみます。

// 証明を命題で注釈します
export const plusZeroLAnn: TermInferable = [
  "Ann",
  plusZeroLProof,
  plusZeroLType,
];
test("check plusZeroL", () => {
  // 証明に命題の型が付くか検査します
  typeInferable(0)([])(plusZeroLAnn);
});

検査を実行します。

   ✓ check plusZeroL 1ms

 Test Files  1 passed (1)

無事に成功しました。これでOKです！

足し算プログラムに要求される性質の1つを、依存型を使って検証したということになります。

ちなみに、命題と証明を合わせたplusZeroLAnnは、JSONで表すと509文字でした。

もう少しむずかしい問題

$0 + n = n$ ができたら、 $n + 0 = n$ もやりたくなるのが人間です。

しかし、その証明は難しいです。先程は、足し算を0に適用したので恒等関数に評価されていました。しかし今回は $n$ に適用するので、そこから先に評価が進みません（ニュートラル項になります）。

コイツを示すには、自然数に対する帰納法が必要です。

// nを受け取って、n + 0 = n型の値を返します
const plusZeroRProof: TermCheckable = [
  "Lam", // arg: n
  [
    "Inf",
    // 自然数の帰納法をnに対して使います
    [
      "NatElim",
      // NatElim_prop
      // 示したい命題です。nを受け取って、n + 0 = n型を返します
      [
        "Lam", // arg: n
        // n + 0 = n型の項（省略）
      ],
      // NatElim_propZero
      // 基底ケース：nがゼロの場合、命題が成り立つことを示す必要があります。今回は0 = 0を示すだけなのでかんたんです
      ["Refl", ["Inf", ["Nat"]], ["Inf", ["Zero"]]],
      // NatElim_propSucc
      // 帰納ケース：nの前者n'があって、prop n'を仮定してprop n、つまりprop (Succ n')型の値を返す必要があります。
      [
        "Lam", // arg: n'
        [
          "Lam", // arg: n' + 0 = n'
          // ここでprop (Succ n')型の値を返すのがゴールです

          // 1. Refl Nat (Succ n')を使って以下が示せます。
          // (Succ n') = (Succ n')
          // 2. 帰納法の仮定「n' + 0 = n'」を使って、左辺のn'をn' + 0に書き換えます
          // (Succ (n' + 0)) = (Succ n')
          // 足し算の定義を思い出すと、これは以下の式と同じです。
          // (Succ (n')) + 0 = (Succ n')
          // 4. これはprop (Succ n')なのでOKです
        ],
      ],
      // NatElim_nat
      ["Inf", ["Bound", 0]], // 帰納法をnに対して使います
    ],
  ],
];

ちなみに、帰納法の中で等式の書き換えが必要ですが、そのためにはeqIndRという別の定理が必要です。eqIndRの詳細は割愛しますが、示すにはEqの帰納法を使います。

$0 + n$ が $n + 0$ になっただけで、帰納法が2つも必要になるのはおもしろいですね。

今回の命題と証明をJSONで表すと、2,366文字でした。

まぁ実際には、足し算の定義が重複して入っているのでもっと短く書けるとは思うのですが、それでも感覚としては先程よりむずかしい問題だったと分かりますね。

最終問題

この記事の冒頭で言っていた、すべての自然数 $n$ について

である証明をやりたいと思います。

流れは以下のようになります。

1. 足し算を定義する
2. 掛け算を定義する
3. $0$ から $n$ までの総和を計算する関数を定義する
4. $x = y$ ならば $y = x$ の証明を書く
5. 等号の書き換えに使う定理の証明を書く
6. $n + 0 = n$ の証明を書く（さっきやったやつです）
7. $(\text{Succ} ~ x) + y = x + (\text{Succ} ~ y)$ の証明を書く
8. $x + y = y + x$ の証明を書く
   • 「 $n + 0 = n$ 」を使う
   • 「 $x = y$ ならば $y = x$ 」を使う
   • 「 $(\text{Succ} ~ x) + y = x + (\text{Succ} ~ y)$ 」を使う
9. $(x + y) + z = x + (y + z)$ の証明を書く
10. $x \times (y + z) = (x \times y) + (x \times z)$ の証明を書く
    • 「 $(x + y) + z = x + (y + z)$ 」を使う
    • 「 $x = y$ ならば $y = x$ 」を使う
    • 「 $x + y = y + x$ 」を使う
11. $n \times 0 = 0$ の証明を書く
12. $n \times 1 = n$ の証明を書く
13. $x \times y = y \times x$ の証明を書く
    • 「 $n \times 0 = 0$ 」を使う
    • 「 $x = y$ ならば $y = x$ 」を使う
    • 「 $n \times 1 = n$ 」を使う
    • 「 $x \times (y + z) = (x \times y) + (x \times z)$ 」を使う
14. $2 \times (0 + 1 + 2 + 3 + \cdots + n) = n \times (n + 1)$ の証明を書く
    • 「 $x = y$ ならば $y = x$ 」を使う
    • 「 $x \times (y + z) = (x \times y) + (x \times z)$ 」を使う
    • 「 $x \times y = y \times x$ 」を使う

やばいです。

工夫したこと

ユーティリティの作成

上記の証明項をすべて手書きしようとするのはマズいです。けが人が出ます。

証明には、長い式がたくさん出現すると予想されますので、そのためのユーティリティを作成しました。例えば、 $x \times (y + z) = (x \times y) + (x \times z)$ という項を書きたいとします。普通に書くと

const expr = [
  "Inf",
  [
    "Eq",
    ["Inf", ["Nat"]],
    [
      "Inf",
      [
        [mulAnn, ":@:", ["Inf", ["Bound", 0]]],
        ":@:",
        [
          "Inf",
          [
            [plusAnn, ":@:", ["Inf", ["Bound", 1]]],
            ":@:",
            ["Inf", ["Bound", 2]],
          ],
        ],
      ],
    ],
    [
      "Inf",
      [
        [
          plusAnn,
          ":@:",
          [
            "Inf",
            [
              [mulAnn, ":@:", ["Inf", ["Bound", 0]]],
              ":@:",
              ["Inf", ["Bound", 1]],
            ],
          ],
        ],
        ":@:",
        [
          "Inf",
          [
            [mulAnn, ":@:", ["Inf", ["Bound", 0]]],
            ":@:",
            ["Inf", ["Bound", 2]],
          ],
        ],
      ],
    ],
  ],
];

めっちゃ長いです。でもmakeEqExprというユーティリティを使うと

const expr = makeEqExpr(
  [["x", "*", ["y", "+", "z"]], "=", [["x", "*", "y"], "+", ["x", "*", "z"]]],
  new Map([
    ["x", ["Inf", ["Bound", 0]]],
    ["y", ["Inf", ["Bound", 1]]],
    ["z", ["Inf", ["Bound", 2]]],
  ])
);

と書けます。

さらに、makeEqExprに渡す配列すら書くのが面倒だったので、テキスト形式で書いてGeminiくんに変換してもらってました。

Rocqでの証明

今回自作した型検査器には、エラーの内容を親切に表示する機能などを付けていません。検査に失敗した場合、どこで失敗したのかがわからないので、証明項を書き間違えたのか、証明そのものの考え方がおかしいのか判断が付きません。

そこで、まず同等の証明を先にRocqで完成させ、そのコードを今回の環境に移植するという方法をとりました。

え？本末転倒じゃないかって？私もちょっと思いました。

ですが今回の目的は、依存型への理解を深めることと、検査器がちゃんと動くかの検証です。

Rocqで書いたのと同等の証明が自作の型検査器でどのように扱われるかは興味深いですし、実際、この証明の最中に検査器のバグをいくつか見つけられました。

証明完成！

   ✓ check main 135ms

 Test Files  1 passed (1)

check mainが、最終問題の証明を検査するテストケースです。検査は135msで完了しました。

ちなみに、命題と証明をJSON文字列にしてみると、576,085文字になります。

ターミナルエミュレータの設定を変更し、文字サイズを1pxにすることで、

すべての項を表示して遊べます。

たのしいですね。

怒られたので設定を戻しました。

発展的な話題

論文の最後の方に、今回の体系は健全ではないことが書かれています。

あまり詳しいことはわからないのですが、どうやらT-Star規則がマズいようで、

$*$ が $*$ 自身に属するので、自己言及のようなことができて、おかしくなってしまうみたいです。

なので、厳密には型検査をパスしても証明が正しいとは言えないです。しかし、今回の目的は依存型を学ぶことなので、考えることを減らして理解に集中できるのはむしろ良かったと思います。

この問題を解決する方法として、グロタンディーク宇宙という考え方があるそうです。意味はまったくわかりませんが、声に出したくなるかっこよさがありますね。

余談：ぼくとGeminiくん

今回の記事を書くにあたって、型付け規則や評価規則をTeX形式に起こすために、論文のPDFからコピーしてきたテキストをGeminiくんに変換してもらっていました。

以下は、T-Pi規則の仮定部分を変換する際にGeminiくんが出してきたDiffですが、

$$
\dfrac
{
-  0 ` ρ ::↓ ∗
-  ρ ⇓ τ
-  0, x :: τ ` ρ′ ::↓ ∗
+  \begin{aligned}
+  & \Gamma \vdash \rho ::_\downarrow * \\
+  & \rho \Downarrow \tau \\
+  & \Gamma, x :: \tau \vdash \rho' ::_\downarrow *
+  \end{aligned}
}
{
+  \Gamma \vdash (\forall x :: \rho. \rho') ::_\uparrow *
}

\quad\text{(T-Pi)}
$$

論文のテキストを与えていない結論部分まで、なぜか完璧に生成しています。

ぼく「結論部分は変換元のテキストを示していないはずですが、あなたは完璧に推論しました。依存関数の型付け規則を知識に持っているということですか……？」

Gemini「はい、ご推察の通り、依存関数の型付け規則に関する知識を持っています。……（中略）……提供されたドキュメント全体の文脈、定義、および他の規則のパターンを総合的に分析することで、欠落している情報を補完することが可能です。」

本記事の内容を読んだそうですが、この時点では抽象構文と、T-Ann、T-Starまでしか書いていなかったので、そこまでの知識から推論したらしいです。すごい。

また、ただ記法を変換するだけではなく

Gemini「T-NatElimの前提は、論文の意図を汲んで整形し、明らかにタイポと思われるm kをm lに修正」

とも言ってきました。

そうなんです。論文には実際にタイポがあって、図と本文を比べるとわかります。

ただ、今回Geminiくんに渡したのは図の情報だけ、つまりタイポがある間違った情報だけでした。当然、TeX記法の間違った式が出てくるはずで、それを手動で修正する想定でした。ところが、規則の意味を解釈したのか「明らかにタイポ」として勝手に正しく修正してしまいました。

さらに、Eqの型付け規則と評価規則に関しては論文にも図がないので、分数表示の雛形だけ用意していて、後で自作する予定でした。しかし、Geminiくんはそこも生成してきました。

結果的には、型付け規則に関してはほぼ正解で、評価規則については全て間違いのようでした。評価の方に関しては、生成の時点で本文中に情報が無かったので、まぁ想定通りです。型付けの方の生成に成功しているのがむしろすごいです。

というわけで、sititou70いらないかもですね。いつの日か、AIが人生を自動化してくれるといいなと思います。

まとめ

依存型がある計算体系について理論を勉強し、それをTypeScriptで実装しました。

• 項、型、カインドの区別がないとどうなるか
• 型を評価するとはどういうことか
• なぜ型検査中に評価が必要なのか

などについて、理解が深まったと思います。

最終的には、足し算、掛け算、総和を実装し、 $0$ から $n$ までの総和に関する命題と証明を構築しました。

この命題は、3年前にはじめて定理証明系というものに触れたときの記事である「Idrisでふんわり眺める依存型」でも取り上げました。同じ命題を自作の検査器でも扱えてうれしいです。

最後に、A tutorial implementation of a dependently typed lambda calculusのおかげで今回の記事が書けました。著者の皆さん、ありがとうございました。

単純型付きラムダ計算を拡張する方法で段階的に説明されており、また実装に困ったらHaskellによるコードも参照できるのでおすすめです。

依存型初心者なので、おかしなところがあれば教えていただけると嬉しいです。

それでは！