自作の定理証明系を弱めてパラドックスを回避しよう

2025/07/29

前回の記事では、依存型を持つ計算体系を論文をもとに写経し、その上で以下の総和の公式を証明しました。

2 \times (0 + 1 + 2 + 3 + \cdots + n) = n \times (n + 1)

しかし一方で、その体系が健全ではないことにも言及していました。

今回は

前回作成した体系が健全ではないことを確認します。ハーケンスのパラドックスを実装し、 $1 = 2$ を証明します。
パラドックスを回避するために、型の階層構造を導入します。
階層構造が導入された体系で、総和の公式は証明できるが、パラドックスが構築できないことを確認します。

前回作成した体系が健全でないことを確認する

前回読んだ論文によれば

Finally, we should reiterate that the type system we have presented is unsound. As the kind of $∗$ is itself $∗$ , we can encode a variation of Russell’s paradox, known as Girard’s paradox [3]. This allows us to create an inhabitant of any type.

訳：最後に、我々が提示した型システムは健全ではないことを改めて強調しておくべきである。 $∗$ のカインド自体が $∗$ であるため、ラッセルのパラドックスの変種であるジラールのパラドックス[3]を符号化することができる。これにより、任意の型の要素を作成できるようになる。

出典：A tutorial implementation of a dependently typed lambda calculus

とのことです。

前回、

\dfrac { } { \Gamma \vdash * ::_\uparrow * } \quad\text{(T-Star)}

がマズそうと言ってたやつですね。

というわけで、ジラールのパラドックスについて調べますと、そのシンプルバージョンであるハーケンスのパラドックスというのがあり、RocqやAgdaで形式化もされているらしいです。シンプルなのは嬉しいですね。

で、さっそくRocqでの形式化を読んでみたのですが、残念ながら全く理解できませんでした。 いかがでしたか？

なんとなくの印象ですが、僕がやりたい事に対してリッチすぎる気がしました。

一方で、Agdaでの形式化の方は結構シンプルで、良さそうな雰囲気です。

ただ残念なことに、僕がAgdaをまったく読めないので、雰囲気しか語れません。

そこで、Geminiくんにお願いして、Agdaでの形式化をRocqのコードに変換してもらったのがsititou70/rocq-hurkens-paradoxです。Rocqにはデフォルトで型の階層構造がありますが、-type-in-typeオプションによってそれを無効化し、今回のパラドックスを構築できます。Geminiくんの出力は、1つの補題（lem3）の証明だけ僕が手で直しましたが、それ以外は一発で検査をパスしました。ほんと優秀ですね〜。

そうして完成した、読みやすく、かつシンプルな形式化により、ハーケンスのパラドックス自体も理解できるようになった わけありませんでした。 個別のコードの流れは分かるのですが、全体としての構成の意味や、その背景にある学問的な気持ちが何も分かりません。初学者なのにこう思うのは、「完全に理解した」の段階にすら行けてないということです。

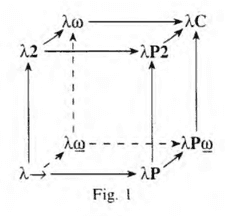
試しに、ハーケンスの元論文である「A simplification of Girard's paradox」を覗いてみたのですが、宇宙語すぎて「へへ……」みたいな謎の笑いしか出ませんでした。純粋型システムであるSystem U（？）とかが使われていて、□とか△とかが楽しそうにしてるねぇという感じでした。

まぁ今回の目標は、パラドックスの理解ではなく駆逐なので、いったん良しとします。

形式化の要点を見てみます。冒頭では、以下のbot型を宣言しています。

Definition bot: Type := forall (A: Type), A.

これは、「Aという型（命題）を受け取って、A型の値（命題の証明）を返す関数の型」という意味です。つまり、どんな命題でも、それを入れたら証明を返してくれる関数の型です。そんな関数が存在したら、その世界ではあらゆる命題が証明可能になるのでおかしいですよね。

そしていろいろあって、形式化の最後の方では、bot型の関数であるloopが得られています。

Definition loop: bot := lem2 lem3.

loopに1 = 2を渡すと、その証明が実際に得られて、検査をパスしてしまいます。

Definition one_eq_two: 1 = 2 := loop (1 = 2).

coqc -type-in-type hurkens.v
# エラーなし。1 = 2が証明された！

これを前回作成した体系に移植したのがlambda-pi/test/paradox/hurkens.test.tsです。こちらでも、無事に（？） $1 = 2$ の証明をパスしました。

const oneEqTwoTerm: TermCheckable = makeApplyExpr(
  loopAnn, // loopに
  makeEqExpr([1, "=", 2], new Map()) // 1 = 2を渡す
);

// ...

// 1 = 2の証明を型検査するとパスする
test("check oneEqTwo", () => {
  typeInferable(0)([])(oneEqTwoAnn);
});

つまり、前回作成した体系は、パラドックスを構築できるほど強すぎるというわけです。

このような体系は、論理体系としては破綻していると言えます。

型の階層構造を導入してパラドックスを回避する

前回読んだ論文の続きによると

To fix this, the standard solution is to introduce an infinite hierarchy of types: the type of $∗$ is $∗_1$ , the type of $∗_1$ is $∗_2$ , and so forth.

訳：これを修正するための標準的な解決策は、型の無限階層を導入することである。つまり、 $∗$ の型は $∗_1$ 、 $∗_1$ の型は $∗_2$ 、というようになる。

出典：A tutorial implementation of a dependently typed lambda calculus

とのことです。

イメージとしては、

*_0 :: *_1 :: *_2 :: \cdots

という制限を加えることで、総和の公式は証明できるが、パラドックスは構築できないように体系を弱めるという感じです。

Designing Dependently-Typed Programming Languagesの講義資料および講義動画を参考にして、型が階層構造を持つように型付け規則と評価規則を修正していきます。資料に情報がない部分については勘でいい感じにしていきます。よろしくおねがいします。

型付け規則

$*$ が現れる規則だけが改造対象です。

一番興味深いのは、T-Star規則です。

\dfrac { } { \Gamma \vdash *_i ::_\uparrow *_{i + 1} } \quad\text{(T-Star)}

$*$ に階層を表す添字が追加されました。あるレベルの $*$ は、その1つ上のレベルの $*$ に属するようになり、それが続いていきます。

T-Starと同じくらい重要なのが、T-Pi規則です。

\dfrac { \begin{aligned} & \Gamma \vdash \rho ::_\uparrow *_i \\ & \rho \Downarrow \tau \\ & \Gamma, x :: \tau \vdash \rho' ::_\uparrow *_j \end{aligned} } { \Gamma \vdash \forall x :: \rho. \rho' ::_\uparrow *_{\text{max}(i, j)} } \quad\text{(T-Pi)}

$\forall x :: \rho. \rho'$ が属する $*$ のレベルは、 $\rho$ と $\rho'$ が属する $*$ のレベルの大きい方になります。

特に注目したいのは、依存関数自体の型のレベルが、引数 $x$ の型のレベルよりも常に大きくなるということです。

例えば、 $x$ として $*_0$ の値を受け取る依存関数があるとします。T-Piの結論より、 $\rho = *_0$ です。T-Piの1行目より $\Gamma \vdash *_0 ::_\uparrow *_i$ を推論します。T-Star規則より $\Gamma \vdash *_0 ::_\uparrow *_1$ となって、 $i = 1$ になります。最終的な依存関数の型は $*_{\text{max}(1, j)}$ となり、 $x$ が属する $*_0$ よりもレベルが大きくなるというわけです。

また細かいのですが、オリジナルのT-Pi規則とは違って、仮定の判別式が推論モードになっています。これは、 $i$ や $j$ の情報がもとの項に無いので仕方ないのですが、実装にじわじわ影響します。詳しくは後述します。

あとの規則はそこまで重要じゃないので畳んでおきます。

あとの規則

まず、 $\text{Nat}$ 型と $\text{Eq}$ 型の型は $*_0$ です。

\dfrac { } { \Gamma \vdash \text{Nat} ::_\uparrow *_0 } \quad\text{(T-Nat)}

\dfrac { \begin{aligned} & \Gamma \vdash a ::_\downarrow *_* \\ & a \Downarrow \tau \\ & \Gamma \vdash x ::_\downarrow \tau \\ & \Gamma \vdash y ::_\downarrow \tau \end{aligned} } { \Gamma \vdash \text{Eq} ~ a ~ x ~ y ::_\uparrow *_0 } \quad\text{(T-Eq)}

ここで、 $*_*$ という新しい記法を導入しました。これは「 $*$ であることを検査するが、レベルは任意である」という意味です。

これは独自の記法です。参考資料では検査ではなく推論を行ったうえで、レベルを無視して $*$ であることだけを確認するような感じになっていました。しかし、実装上の都合からこのようにしました。詳しくは後述します。

残りの規則に関しては、仮定部分に $*_*$ が現れるだけでオリジナルと同じです。

\dfrac { \begin{aligned} & \Gamma \vdash \rho ::_\downarrow *_* \\ & \rho \Downarrow \tau \\ & \Gamma \vdash e ::_\downarrow \tau \end{aligned} } { \Gamma \vdash (e :: \rho) ::_\uparrow \tau } \quad\text{(T-Ann)}

\dfrac { \begin{aligned} & \Gamma \vdash p ::_\downarrow \text{Nat} \rightarrow *_* \\ & (p ~ \text{Zero}) \Downarrow \tau \\ & \Gamma \vdash pz ::_\downarrow \tau \\ & \forall l :: \text{Nat}. p ~ l \rightarrow p ~ (\text{Succ} ~ l) \Downarrow \tau' \\ & \Gamma \vdash ps ::_\downarrow \tau' \\ & \Gamma \vdash k ::_\downarrow \text{Nat} \end{aligned} } { \Gamma \vdash \text{natElim} ~ p ~ pz ~ ps ~ k ::_\uparrow p ~ k } \quad\text{(T-NatElim)}

\dfrac { \begin{aligned} & \Gamma \vdash a ::_\downarrow *_* \\ & a \Downarrow \tau \\ & \Gamma \vdash x ::_\downarrow \tau \end{aligned} } { \Gamma \vdash \text{Refl} ~ a ~ x ::_\uparrow \text{Eq} ~ a ~ x ~ x } \quad\text{(T-Refl)}

\dfrac { \begin{aligned} & \Gamma \vdash a ::_\downarrow *_* \\ & a \Downarrow \tau_a \\ & \Gamma \vdash p ::_\downarrow \forall x :: \tau_a. \forall y :: \tau_a. \text{Eq} ~ a ~ x ~ y \rightarrow *_* \\ & \forall z :: \tau_a. \tau_p ~ z ~ z ~ (\text{Refl} ~ a ~ z) \Downarrow \tau_{pr} \\ & \Gamma \vdash pr ::_\downarrow \tau_{pr} \\ & \Gamma \vdash x ::_\downarrow \tau_a \\ & \Gamma \vdash y ::_\downarrow \tau_a \\ & \Gamma \vdash eqxy ::_\downarrow (\text{Eq} ~ \tau_a ~ x ~ y) \end{aligned} } { \Gamma \vdash \text{eqElim} ~ a ~ p ~ pr ~ x ~ y ~ eqxy ::_\uparrow p ~ x ~ y ~ eqxy } \quad\text{(T-EqElim)}

評価規則

特に面白くないのですが、いちおう完全のために載せておきます。

\dfrac { } { *_i \Downarrow *_i } \quad\text{(E-Star)}

$*_i$ は評価しても $*_i$ です。

実装

まずはじめに、構文としてもStarにレベルを導入します。

export type TermInferable =
// ...
- | ["Star"]
+ | ["Star", number]

これにより、プログラム中のStarと書いていた部分に、明示的にレベルの指定が必要になります。

Rocqでは Type と書く時にレベルを指定する必要はありませんが、それはRocqがよしなにレベルを推定してくれているからだそうです。

また、1つのプログラムを複数のレベルでインスタンス化するという機能（宇宙多相）もあるのだそうです。今回の体系には、もちろんそんな高度な機能は無いので、実際にハーケンスのパラドックスを持ってくる際には、似たようなコードを重複して書く必要がありました。ただ、総和の公式の証明ではそのような必要はなかったので、宇宙多相が無いことは、自然数に対する通常の証明を書く上ではそこまで問題にならないようでした。

Starの階層構造が導入できたら、あとは各規則を愚直にコードへ落とし込んでいくことになります。

ただ、T-Piの仮定の判別式については、もともと検査モードだったのが推論モードになっています。なので、依存関数の構文も同時に変更しないといけません。

export type TermInferable =
// ...
- | ["Pi", TermCheckable, TermCheckable]
+ | ["Pi", TermInferable, TermInferable]

こうすると、検査器やユーティリティはもちろん、既存の証明（プログラム）コードも変更しないといけないので大変です。また、一部のユーテリティ（quote）の実装が非常に難しくなってしまい、別の方針のユーテリティを書くことになったりしました。なので、構文の変更というのはできるだけやりたくありません。

T-Pi以外にも、 $*$ が現れる規則はいくつかあるのですが、それらの規則では、T-Piのようにレベルを変数に束縛して結論で使いたいというわけではなく、単純に「何らかのレベルの $*$ であることを検査したい」だけのようでした。

そのような場合、講義資料では「型を推論して、その型が $*$ であることを確認する（レベルは無視する）」という動作でした。

今回の実装では、「型を検査するのはそのままで、検査器自体の動作を変更することで、その型が $*$ であることを確認する（レベルは無視する）」という動作にしました。また、そういう動作が必要なことを表す、検査器内部でだけ使用する特殊な構文 $*_*$ も定義しました。

どちらの方法で実装しても、検査の内容としては同等だと思います。講義資料の方が定義としてはきれいだと思いますが、今回は実装の簡単さと、元論文との対応を維持するために後者の方法を選択しました。

階層構造が導入された体系で、パラドックスが構築できないことを確認する

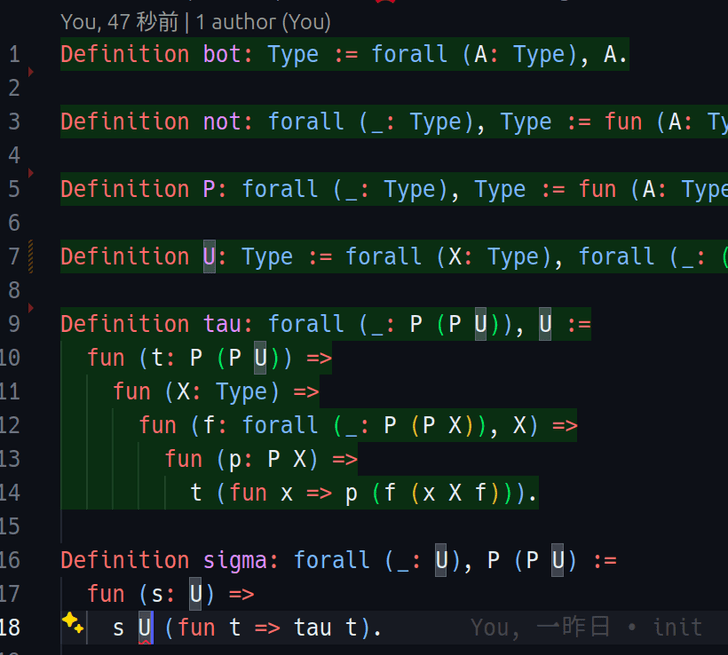
これは通常の（Type in Typeではない）Rocqでハーケンスのパラドックスを検査しているところです。

bot、not、P、U、tauというように、必要な項を次々定義していますが、sigmaという項は定義できていません。

なぜsigmaが定義できないのかというと、型の階層構造によって一種の自己適用が禁止されるからです。

sigmaの... fun (s: U) => s U ...という記述がエラーを起こしている部分です。s Uという適用があるので、sは関数です。Uはsの型なので依存関数型です。s Uという適用では、U自体が引数としてsに渡されています（一種の自己適用）。

ここで、T-Piにより、Uの型のレベルは、引数の型のレベルよりも大きくなります。例えば、Uの型のレベルが $*_1$ 、引数の型のレベルが $*_0$ みたいになります。Uの型のレベルが $*_1$ なので、U自身は $*_0$ となります。Uの引数として渡せるのは、引数の型に属する要素だけです。つまり $*_0$ （U自身） $::$ $*_0$ （引数の型）が要求されるのですが、これは拒絶されるので、Uは引数として渡せず、パラドックスが回避されるというわけです。

詳しくはコード上のコメントに書きました。動作を理解するために、簡略化したUとsを定義して、実際に自己適用ができないのをテストしています。また、bot〜tauまでの定義が検査をパスするのも確認しました。

まとめ

というわけで、めでたく、ハーケンスのパラドックスは構築できなさそうというのがわかりました。

一方、総和の公式の証明は、そのまま移植して検査をパスするのを確認できましたので、目標達成です。

ちなみに、階層構造を導入する前の前回の体系で、 $1 = 2$ の証明項を確認すべく評価してみると、

evalInferable(oneEqTwoAnn)([]);
// RangeError: Maximum call stack size exceeded

スタックを突き破ってエラーになってしまいました。実質的に無限ループが発生しているようです。

無限ループによってあらゆる命題が証明できてしまうというのは、TAPLにある「不動点コンビネータに型付けできるとすべての命題が証明可能になってしまう話」に似ているなと思いました。↑のリンクは、以前カワるガワるTAPLカタるヨるというイベントに呼んでいただいた際に発表した資料です。

不動点コンビネータはラッセルのパラドックスと関係しているという話もありますし、ここらへんの自己言及の親戚たちは、おそらく原理的には同じような仕組みを持っているんだろうな〜〜という気持ちになりました。

もちろん、今回の修正によって体系が健全になったとは言えないです。厳密にはちゃんと健全性を証明しないといけないし、けっこう勘でいろいろいじくったので、どこかおかしくしてしまった可能性は十分あります。

なので、間違いとかツッコミがあれば教えていただけると助かります。

ありがとうございました。

自作の定理証明系を弱めてパラドックスを回避しよう

前回作成した体系が健全でないことを確認する

型の階層構造を導入してパラドックスを回避する

型付け規則

評価規則

実装

階層構造が導入された体系で、パラドックスが構築できないことを確認する

まとめ

続けて読む…

自作してふんわり眺める依存型【定理証明】

ラムダ計算で型のリハビリ

ざっくりホーア論理

TypeScriptの型で全加算器から浮動小数点数，そして√2

BlenderとEeveeで地球

Advent of Code 2021攻略ガイド