夏なのに引きこもりなので花火を作ります.
花火の作成
なにはともあれ,まずは花火の表現方法を考えます.結果だけ知りたい方はジオメトリノードを構築まで飛ばしてください.
採用しなかった方法:物理演算とモーションブラー
花火の運動を再現したい場合,真っ先に思いつくのはBlenderのパーティクル鋼体シミュレーションです.ちょっと実験してみましょう.

まぁこんな結果になるんですが,写真としては違和感があります.というのも,「花火大会」で画像検索してみると……
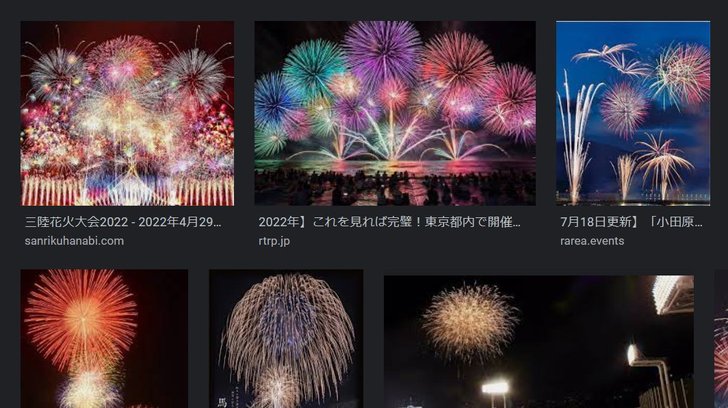
写真の花火は,「点」ではなく「線」で写っています.
これは,撮影時に露光時間を長く取っているためです.
開花した花火が消えるまでシャッターを開いておくと、(中略)花火の軌跡をきれいに捉えることができます。シャッター速度が短すぎると(中略)花火が点で写ってしまいます。

出典: 花火大会の彩りを撮る, ソニー
というわけで,「Blender シャッタースピード」とか「Blender 長時間露光」で検索してみると,「モーションブラーを使え」との記述が出てきます.実際に使ってみると,

……あれ?なんだかガビガビです.
私の設定が悪いのかもしれませんが,どう頑張っても綺麗な結果は得られませんでした.
また,この方法では不便な点が多いように感じます.レンダリングしないと軌跡の形がわからないし,マテリアルの調整も大変そうです.
他にも,パーティクルの数を増やしたり,子パーティクルを設定したりして擬似的に軌跡を表現する方法も試しましたが,どれもきれいな結果にはなりませんでした…….
採用した方法:運動方程式+ジオメトリノード
一番良いのは,鋼体の軌跡をメッシュとして直接得られることです.
そもそも,花火の動きは単純なので,時刻からその星(空中で光る火薬1つ)の位置を代数的に決定できるはずです.つまり,ステップバイステップの数値解析は必要ありません.
したがって,運動方程式を解いて星の位置を直接計算し,ジオメトリノードによって花火のメッシュを生成します.
運動方程式を解く
変数や関数を以下のように定義します.
- t:花火が開く瞬間を0とする時刻,s
- m:星の質量,kg
- k:空気抵抗係数,スカラー
- 加速度
- a(t):時刻tにおける星の加速度ベクトル,(m/s2,m/s2,m/s2)
- ax(t):時刻tにおける星の加速度ベクトルのx成分,m/s2
- g:重力加速度,(m/s2,m/s2,m/s2)
- 速度
- v(t):時刻tにおける星の速度ベクトル,(m/s,m/s,m/s)
- vx(t):時刻tにおける星の速度ベクトルのx成分,m/s
- v0:時刻0における星の速度ベクトル,(m/s,m/s,m/s)
- v0x:時刻0における星の速度ベクトルのx成分,m/s
- 位置
- p(t):時刻tにおける星の位置ベクトル,(m,m,m)
- px(t):時刻tにおける星の位置ベクトルのx成分,m
- p0:時刻0における星の位置ベクトル,(m,m,m)
- p0x:時刻0における星の位置ベクトルのx成分,m
星の運動方程式は重力と空気抵抗を用いて以下のようになります.
ma(t)=mg−kv(t)
両辺をmで割れば,
a(t)=g−mkv(t)
加速度a(t)が得られます.
ここからは,ひとまずx成分に着目して解いていくことにします.
ax(t)=gx−mkvx(t)
簡単のために,r=mkとおきます.
ax(t)=gx−rvx(t)
これをtで積分して速度vx(t)を求めます.変数分離を使います.
ax(t)dtdvx(t)dtdvx(t)vx(t)−rgx1dtdvx(t)vx(t)−rgx1dvx(t)∫vx(t)−rgx1dvx(t)log{vx(t)−rgx}vx(t)−rgxvx(t)−rgxvx(t)=gx−rvx(t)=gx−rvx(t)=−r{vx(t)−rgx}=−r=−rdt=∫−rdt=−rt+C1=e−rt+C1=e−rteC1=e−rteC1+rgx(1.1)
C1は積分定数です.
ここで,vx(0)=v0xより
vx(0)eC1+rgxeC1=v0x=v0x=v0x−rgx(1.2)
となるため,(1.2)で(1.1)を書き換えると
vx(t)=e−rt(v0x−rgx)+rgx
となり,速度vx(t)が得られました.
これを更にtで積分することで,位置px(t)を求めます.
vx(t)dtdpx(t)px(t)px(t)px(t)px(t)=e−rt(v0x−rgx)+rgx=e−rt(v0x−rgx)+rgx=∫{e−rt(v0x−rgx)+rgx}dt=∫e−rt(v0x−rgx)dt+∫rgxdt=(v0x−rgx)∫e−rtdt+∫rgxdt=−r1(v0x−rgx)e−rt+rgxt+C2(2.1)
C2は積分定数です.
ここで,px(0)=p0xより
px(0)−r1(v0x−rgx)+C2C2=p0x=p0x=r1(v0x−rgx)+p0x(2.2)
となるため,(2.2)で(2.1)を書き換えると
px(t)px(t)=−r1(v0x−rgx)e−rt+rgxt+r1(v0x−rgx)+p0x=r1(v0x−rgx)(1−e−rt)+rgxt+p0x
となり,位置px(t)が得られました.
y成分とz成分についても同様なので,時刻tにおける位置p(t)は次のようになります.
p(t)=r1(v0−rg)(1−e−rt)+rgt+p0
ただし
です.
ジオメトリノードを構築
以下が最終的なジオメトリノードです.(画像をクリックすると拡大します)
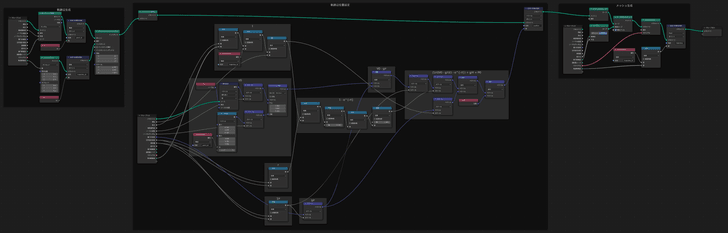
このノードは,面から法線方向に星を射出します.そのため,球以外にも様々なジオメトリを入力することで,ほとんどの種類の花火を表現できます.
使用例
例えば次のような設定の花火ジオメトリノードを球に適用します.横向きの重力加速度は横風を意図しています.
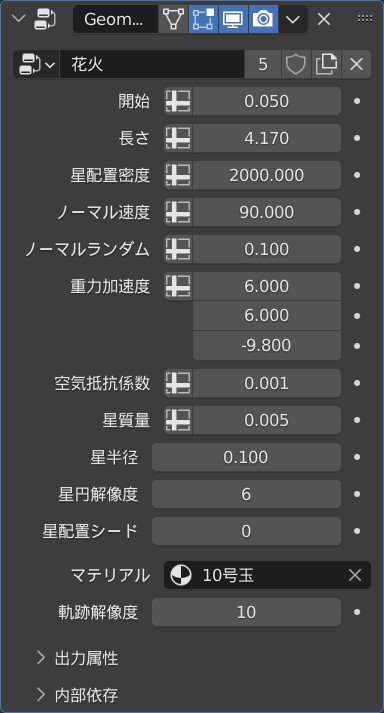
ジオメトリノードの結果,以下のようなそれっぽいメッシュが得られます.

それっぽいですね.
解説
各部分について細かく説明していきます.
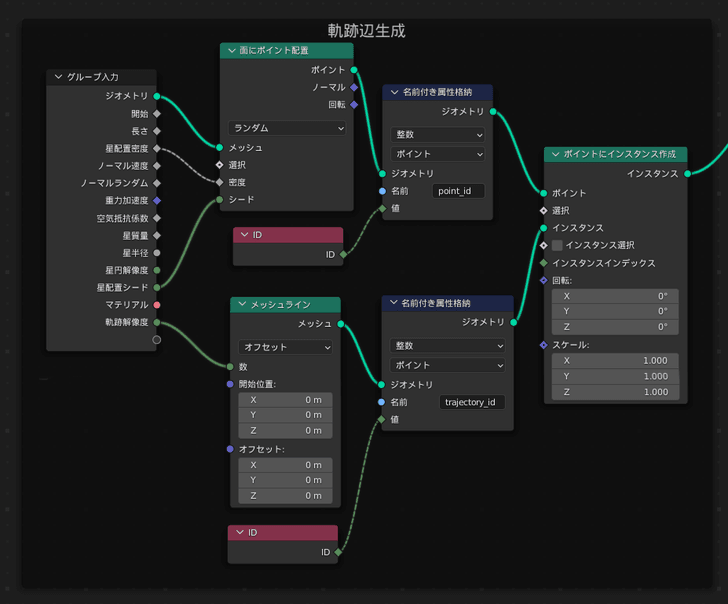
上図では,軌跡の辺を生成しています.「面にポイント配置」によって,星を配置する場所をランダムに決めています.「メッシュライン」によって,星の軌跡を表現します.なお,ポイントとメッシュラインそれぞれでIDを格納しておきます.
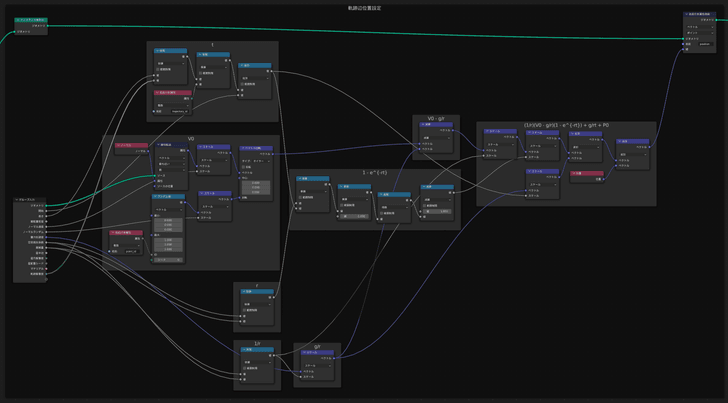
上図では,先程求めたp(t)を使って軌跡の位置を計算しています.tはメッシュラインが生成した各頂点のIDを使って算出されます.v0は面のノーマルとノーマル速度から与えられます.また,v0を任意の係数でランダマイズする機能もあり,軌跡が単調になるのを防ぎます.
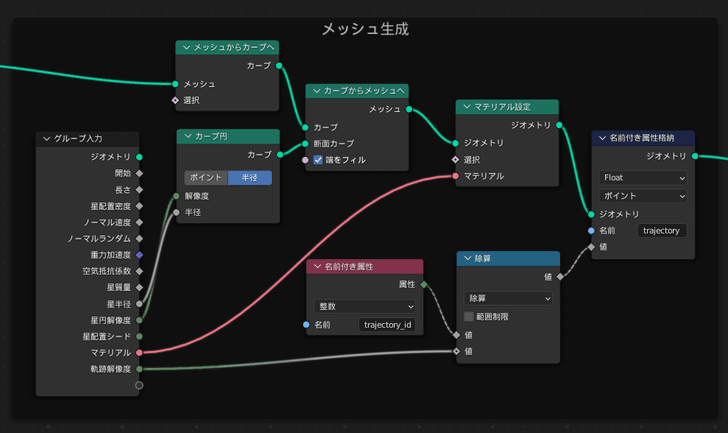
上図では,メッシュをソリッド化しています.そのためにメッシュを一旦カーブに変換し,そのうえで断面カーブを指定することで再度メッシュに戻しています.最後に,trajectoryという値を格納しています.これは,軌跡の始まりが0,終わりが1になるような値です.後のマテリアル設定で使います.
花火マテリアル
以下のようになりました.
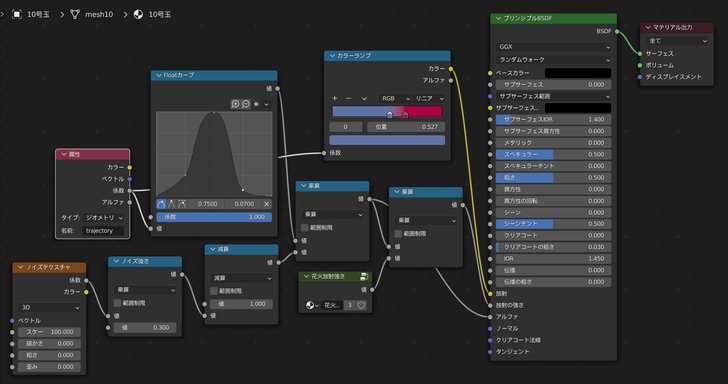
ポイントは,先程のジオメトリノードで格納したtrajectoryを使って放射強度や色を制御しているところです.
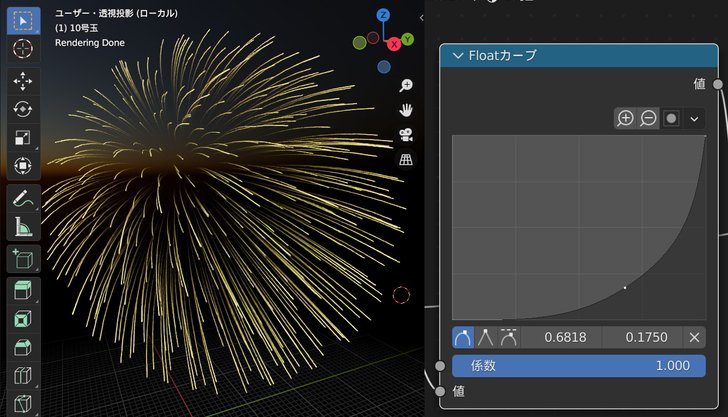
例えば,放射強度が固定値だと以下のような単調な見た目になってしまいます.

この値をカーブでいじってやることで,軌道の尾をフェードアウトさせたり,
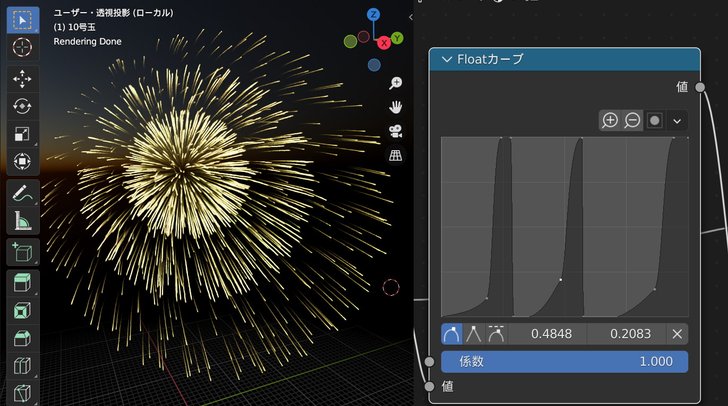
多重の花火(八重芯,三重芯,四重芯……)を表現したりできます.
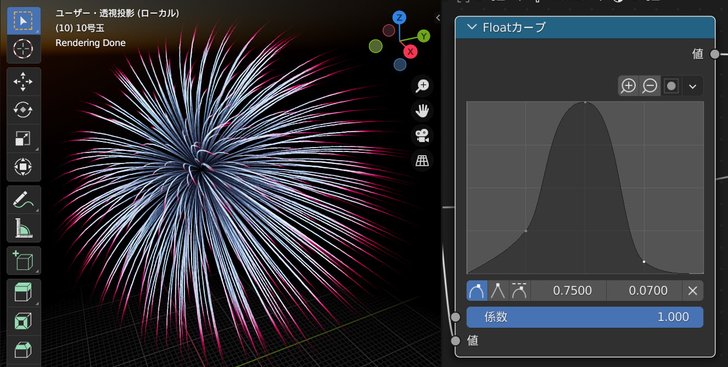
今回は,尾と先端をフェードさせるシンプルな表現にしました.
シーンレイアウト
以下のようにしました.
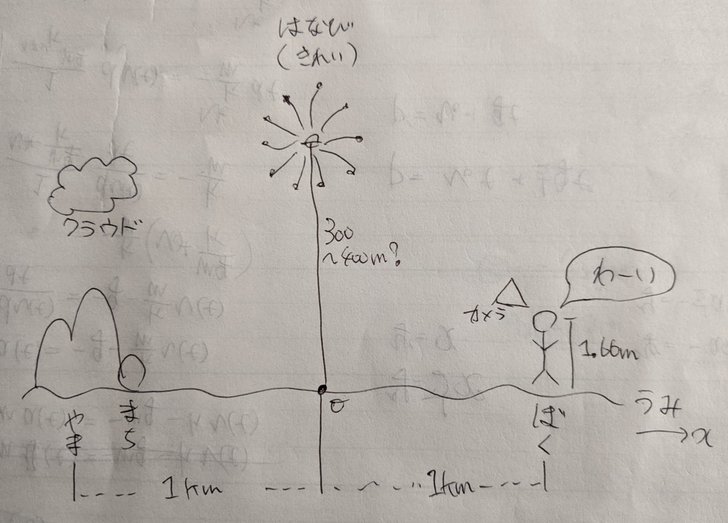
海の上に山が乗っかってるのは,作図が雑だからです.
ともかく,Blenderに実装するとこうなります.
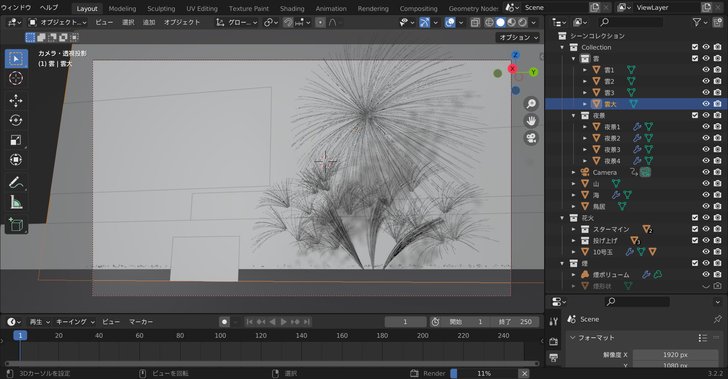
山や雲は画像です.以下のフリー素材を使用させていただきました.
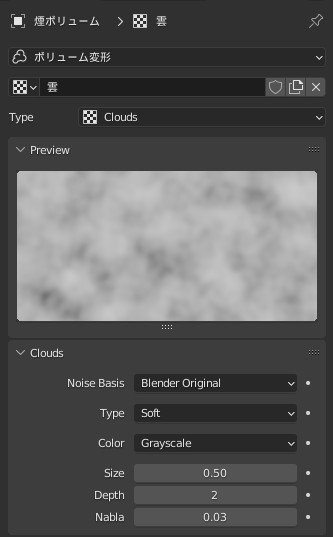
花火の煙は,「メッシュのボリューム化」と「ボリューム変形」モディファイアで適当に作りました.
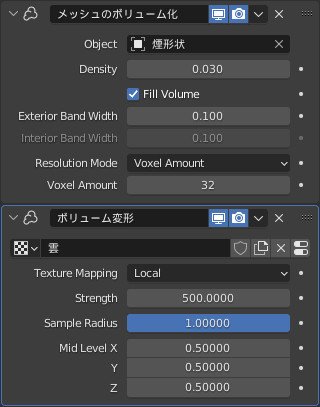
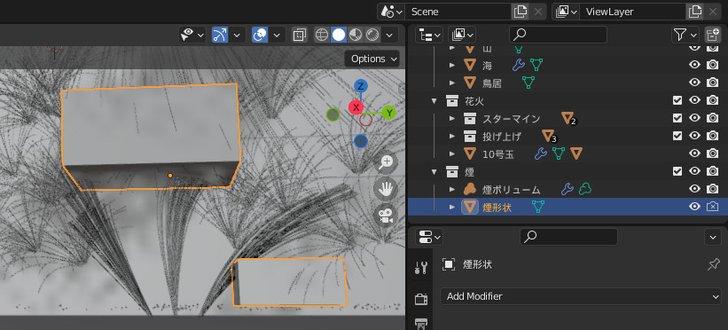
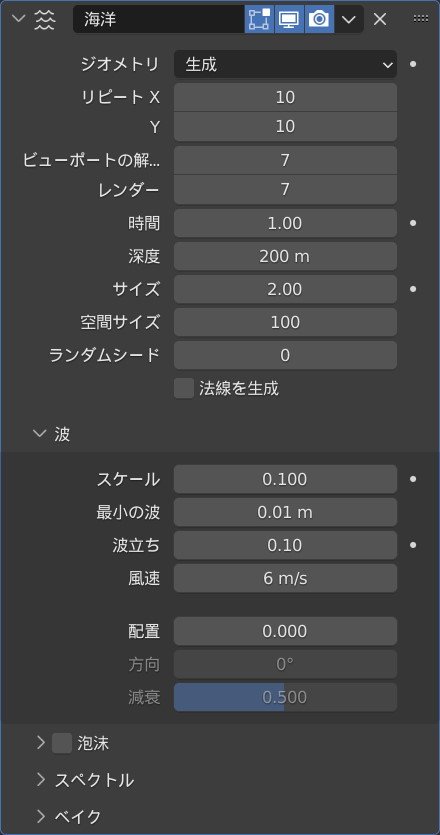
海はオーシャンモディファイアを使用して作りました.
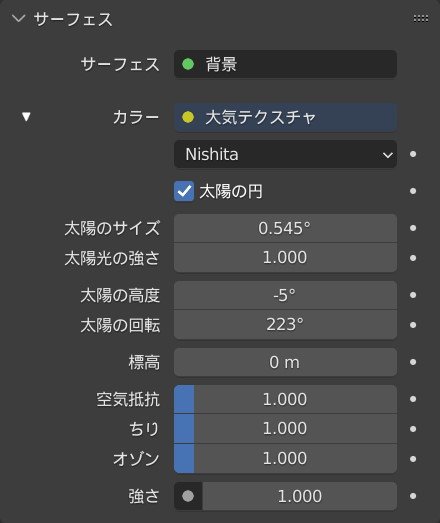
環境は,例のごとく西田先生の大気テクスチャにお世話になります.フォトリアリスティック自宅でも使用したやつです.
レンダリングとコンポジット
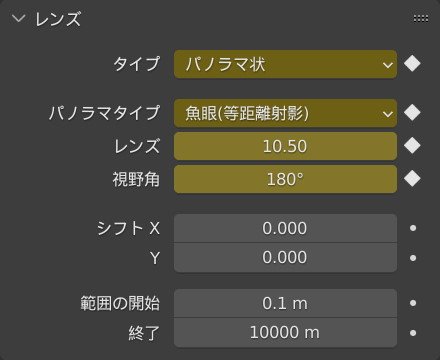
まずカメラの設定です.今回は広範囲を撮影するので,その広さが伝わるように,魚眼レンズで撮影し画面を歪ませています.
次にコンポジットの設定です.以下のようになりました.
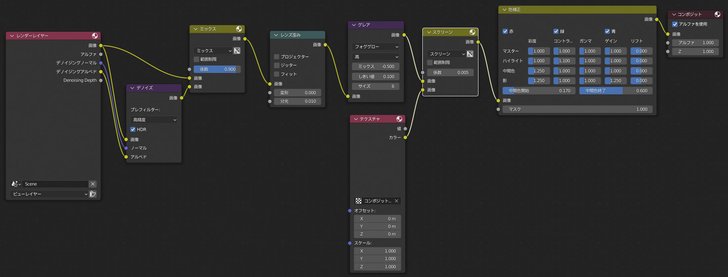
デノイズ処理をしたうえで色収差,グレイン,グローを再現しています.
被写界深度と周辺減光に関しては,撮影範囲が広いこと,露光時間が長いことを考慮して,あえて再現しませんでした.
完成
↓全体像(4K撮影)

↓上から見た図

↓下(発射地点)から見た図

まぶし!
まとめ
Blenderで夏の花火大会を開催しました.
花火の軌跡を表現するために,物理モデルを組み込んだジオメトリノードを構築しました.運動方程式や微分積分など,学生の頃は「なんの役に立つんだ?」と思っていた知識が,こうして納涼に役立つわけですから面白いですね.
ありがとうございました.
参考文献